Archimedes knew the volume of a sphere
. . . now he had to prove it!  

Archimedes built a sphere-like shape from cones and frustrums (truncated cones)

He drew two shapes around the sphere's center -

one outside the sphere (circumscribed) so its volume was greater than the sphere's,  and one inside the sphere (inscribed) so its volume was less than the sphere's.

Here is a bad example, an inscribed shape made of 2 cones and just 2 frustrums

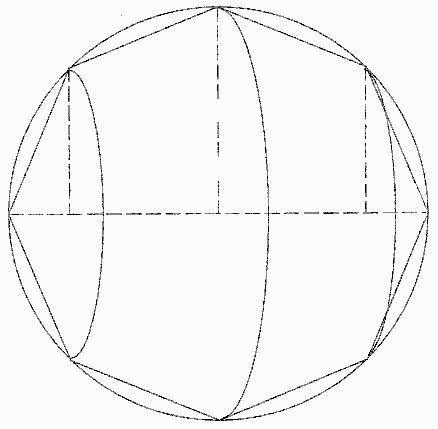
The more frustrums the shape has, the more it looks like a sphere.

This argument allowed Archimedes to rigorously determine
both the volume and surface area of a sphere!

back | next | index