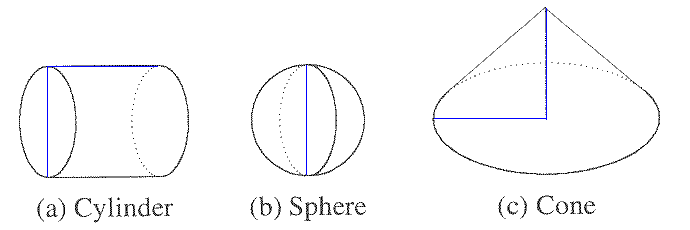
Archimedes balanced a cylinder, a sphere, and a cone. All of the dimensions shown in blue are equal.

Archimedes specified that the density of the cone is four times the density of the cylinder and the sphere.
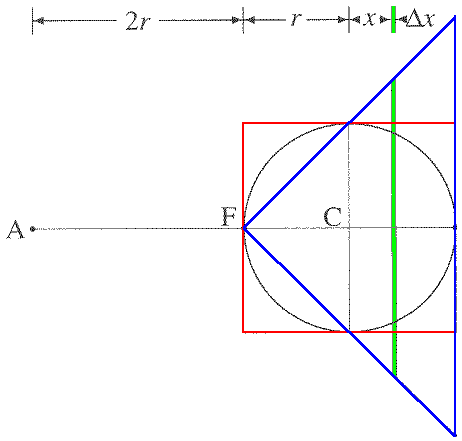
Archimedes imagined taking a circular
slice out of all three solids.
He then imagined hanging the cylinder and the sphere from point A and suspending the solids at point F (the fulcrum).