1. Both Ptolemy (2nd cent. AD) and Copernicus (16th cent. AD) constructed models of the solar system, and their systems were equally successful in predicting the positions of the planets in the sky. However, their two systems were quite different:

a. In Ptolemy's solar system, Earth was at the center.

b. In Ptolemy's solar system, the planets move around a small circle called an epicycle. This small circle moved around Earth on a large circle called a deferent. These circles were used by Ptolemy to explain the retrograde motion of the planets.

c. In Copernicus' solar system, the planets travel in elliptical orbits around the Sun.

d. In Copernicus' solar system, retrograde motion results from Earth overtaking and passing a more slowly moving superior planet. In this way, relative to the distant background stars, planets appear temporarily to reverse their usual eastward direction of motion, and move westward.

Also, according to Copernicus= heliocentric system, the daily motion of the heavens (all heavenly objects rise in the east and set in the west) is explained by Earth= s rotation on its axis.

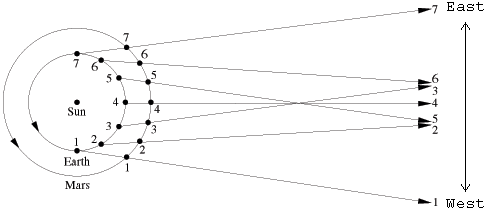
2. Earth and Mars are shown in their orbits around the Sun; 7 positions are shown for each planet. For each pair of positions, an arrow is drawn from Earth, through Mars, out toward the east-west direction line. Identify the two time intervals (such as 1 -> 2) when Mars exhibits retrograde motion (when it appears to move westward).

3 -> 4

and

4 -> 5

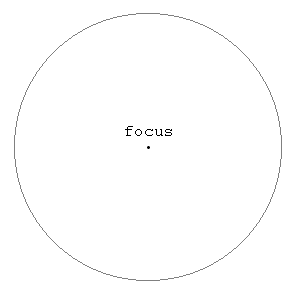
3. Use the scale below to make measurements and calculate the eccentricity of the two ellipses below.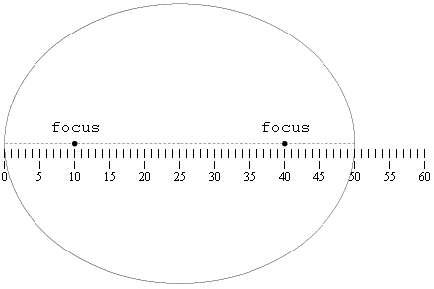

               distance between foci = 30

               length of major axis = 50

eccentricity = 0                           eccentricity = 0.6

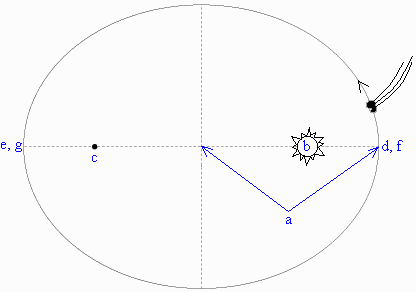
4. This drawing shows the elliptical orbit of a comet around the Sun. Identify a) the semimajor axis; b) the focus where the Sun is located; c) the empty focus; d) perihelion; e) aphelion; f) the point where the comet moves fastest; and g) the point where the comet moves slowest.

5. Kepler's third law tells how long it take an object to orbit the Sun. The time for one orbit is the sidereal period P, measured in years. P is given by  

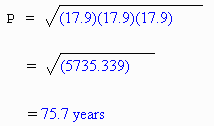
6. Write down Newton's first law of motion:

An object at rest remains at rest, and an object in motion remains in  motion (same speed and direction), unless an unbalanced force acts on the object.

Is an unbalanced force acting on any of the objects below? If so, draw an arrow showing the direction of the unbalanced force.

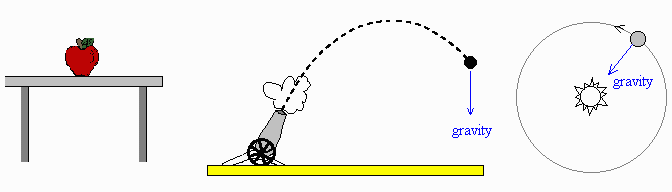
a) an apple sitting    b) a cannonball shot   c) the Earth orbiting
   at rest on a table     from a cannon          the Sun

7. Write down Newton's second law of motion:

Newton's second law explains why all objects fall with the same acceleration. An object A that has twice the mass of another object B weighs twice as much. That is, the force of gravity acting on object A is twice the force of gravity acting on object B.  According to Newton's second law, twice the force acting on twice the mass produces the same acceleration, so objects A and B fall with the same acceleration.

8. Write down Newton's third law of motion:

If I push you with a force, you push me back (opposite direction) with the same strength force.

This explains why Earth orbits the Sun, instead of the Sun orbiting Earth. Newton's third law says that Earth and the Sun attract each other with gravitational forces of the same strength. But Earth has a much smaller mass than the Sun, so that (according to Newton's second law) Earth will have a much larger acceleration than the Sun. Thus it is that Earth moves around the Sun, rather than vice versa.

9. Gravity is the force that keeps the planets in their orbits around the Sun. It also keeps the Moon and spacecraft in their orbits around Earth. Astronauts in an orbiting spacecraft have not escaped Earth's gravity. They appear "weightless" because they and their spacecraft are all falling around the Earth, and all objects fall with the same acceleration.

Dr. Kathryn C. Thornton, astronaut ->