PHYSICS 1040 - ELEMENTARY ASTRONOMY - HOMEWORK #13

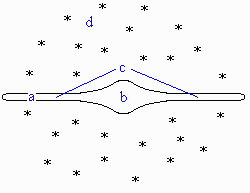1. This is an edge-on view of our Milky Way galaxy. Identify a) the position of the Sun (8 kpc from the center); b) the galactic nucleus; c) the galactic disk; and d) the galactic halo of globular clusters. The Milky Way galaxy is about 50 kpc is diameter, and the disk is about 0.6 kpc thick.

 

 

 

 

2. Very hot, luminous O and B-stars are seen only in the spiral arms of our Milky Way galaxy. These stars have very short/long (circle one) lifetimes; they do not live long enough to travel very far from their birthplace. This tells astronomers that stars are formed in the spiral arms of our Milky Way galaxy.
 

 

3. The spiral arms of our galaxy are caused by spiral density waves. The stars orbiting the galactic nucleus obey Kepler's first law; the shape of their orbits is an ellipse. The axis of each orbit is precessed; each one has a slightly different direction. This produces an overall spiral pattern (see below). Trace the spiral pattern on the diagram on the right. The spiral pattern is where stars and gas happen to come closer together in a spiral density wave. This compression causes interstellar clouds to collapse and form stars.

 

 

 

 

 

 

 

 

4. The object located at the center of our Milky Way galaxy is called Sagittarius A*. What evidence do astronomers have that Sgr A* is a supermassive black hole having 2.6 million solar masses?

a. vast amounts of radio wave energy come from Sgr A*

b. all the gas within about 2 parsecs of Sgr A* is ionized

c. high-speed stars and gas held in orbit around Sgr A* by an immense gravitational force
 

5. Kepler= s 3rd law, as derived by Newton, says that a3/P2 = (M1 + M2), where a is the semimajor axis of the orbit of the two stars (in AU), P is the period of the orbit (in years), and M1 and M2 are the masses of the two stars (in Mu , solar masses). A star named S2 orbits the supermassive black hole at the center of our Milky Way galaxy with a period of P = 15.2 years. If the semimajor axis of the star= s orbit is a = 840 AU, then the sum of the masses of the two stars is a3/P2 = (840)3/(15.2)2 = 2.6 million Mu . If we ignore the mass of S2 as being negligibly small, then we can conclude that the mass of the supermassive black hole is 2.6 million Mu.
 

6. The most distant Cepheid variable yet observed (in a galaxy called NGC 4603) has a pulsation period of 60 days. Using the period-luminosity relation on Homework #11, this star is found to have an absolute magnitude of M = -6.3. This star has an apparent magnitude m = 26.3. How far away is this Cepheid variable? In Question #10 on Homework #4, we found that if a star has apparent magnitude m and absolute magnitude M, then the distance d (in parsecs) to the star is

d (parsecs) = 10[m - M + 5]/5.

In this case, m = 26.3 and M = -6.3, so

[m - M + 5]/5 = [(26.3) - (-6.3) + 5]/5 = [37.6]/5 = 7.52.

Thus d = 10[m - M + 5]/5 = 33.1 million parsecs. Since 1 parsec = 3.26 light years, we find d = 108 million light years.

Most supernovae have about the same absolute magnitude at peak brilliance, M = -19.5. The most distant supernova yet observed has an apparent magnitude m = 23.2. How far away is this supernova? If a star has apparent magnitude m and absolute magnitude M, then the distance d (in parsecs) to the star is d (parsecs) = 10[m - M + 5]/5. In this case, m = 23.2 and M = -19.5, so

[m - M + 5]/5 = [(23.2) - (-19.5) + 5]/5 = [47.7]/5 = 9.54.

Thus d = 10[m - M + 5]/5 = 3.47 billion parsecs. Since 1 parsec = 3.26 light years, we find d = 11.3 billion light years.
 

7. In 1929, Edwin Hubble discovered that the universe is expanding. There is no center to this motion; every galaxy is moving away from every other galaxy. Astronomers on Earth therefore see every galaxy moving away from us. This motion is a special one, with galaxies twice as far from us moving away twice as fast. We are/are not (circle one) at the center of the expansion because an observer in any other galaxy would see the same expansion that we see.

The Hubble constant H0 tells how fast the distant galaxies are receding. If H0 = 71 km/sec/Mpc (1 Mpc = 1 million parsecs), then a galaxy that is 10 Mpc away has a speed of 710 km/sec, and a galaxy that is 20 Mpc away has a speed of 1420 km/sec. On the other hand, if the speed of a galaxy is known (from the Doppler-shifted absorption lines in its spectrum), then Hubble's Law tells the distance to that galaxy. This is how the distances to the farthest objects in the universe are measured.


8.


 

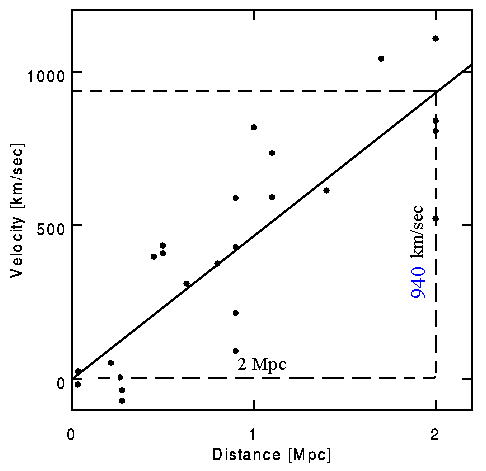
The diagram above shows Hubble= s original data from 1929. The Hubble constant H0 is the slope of the line through Hubble= s data. Thus Hubble= s own value for H0 was

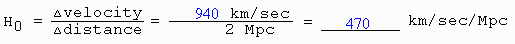
This is much larger than the present value of 71 km/sec/Mpc! (Hubble mistakenly used another type of variable star instead of the Cepheids we have discussed in class.)

9. Galaxies are not A island universes.@ Galaxies are gravitationally bound in associations called clusters. Our Milky Way galaxy belongs to a poor cluster of about 30 members called the Local Group. Galaxies in the same cluster may collide and sometimes even merge together. Such mergers may be responsible for creating the giant elliptical galaxies that are found in the centers of many rich clusters of galaxies. Clusters form even larger associations called superclusters. These superclusters are found in the walls of vast, nearly empty regions called voids. These roughly spherical voids are around 30 - 120 Mpc across.
 

10. Astronomers observe that the stars in the inner/outer (circle one) part of the disk of spiral galaxies (including our Milky Way galaxy) orbit the galactic nucleus slower/faster (circle one) than expected from Kepler= s laws. This is evidence that our Milky Way galaxy and other galaxies are surrounded by vast quantities of dark matter. Further evidence of dark matter comes from observations of massive galaxies and clusters of galaxies. If the light rays from a distant object pass by an extremely massive galaxy or cluster on their way to Earth, the light rays will be bent as they travel through the curved space surrounding the massive galaxy or cluster. The light rays will be brought to a focus and produce images of the distant object. This is called a gravitational lens. From the positions of the images, the total mass of the massive galaxy or cluster can be determined. Astronomers have found that about 90 percent of the total mass of a massive galaxy or cluster is in the form of dark matter.

 

Return to Phys 1040 home page