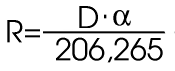
The Ring Nebula. Image credit: Heritage Project, STScI
Summary

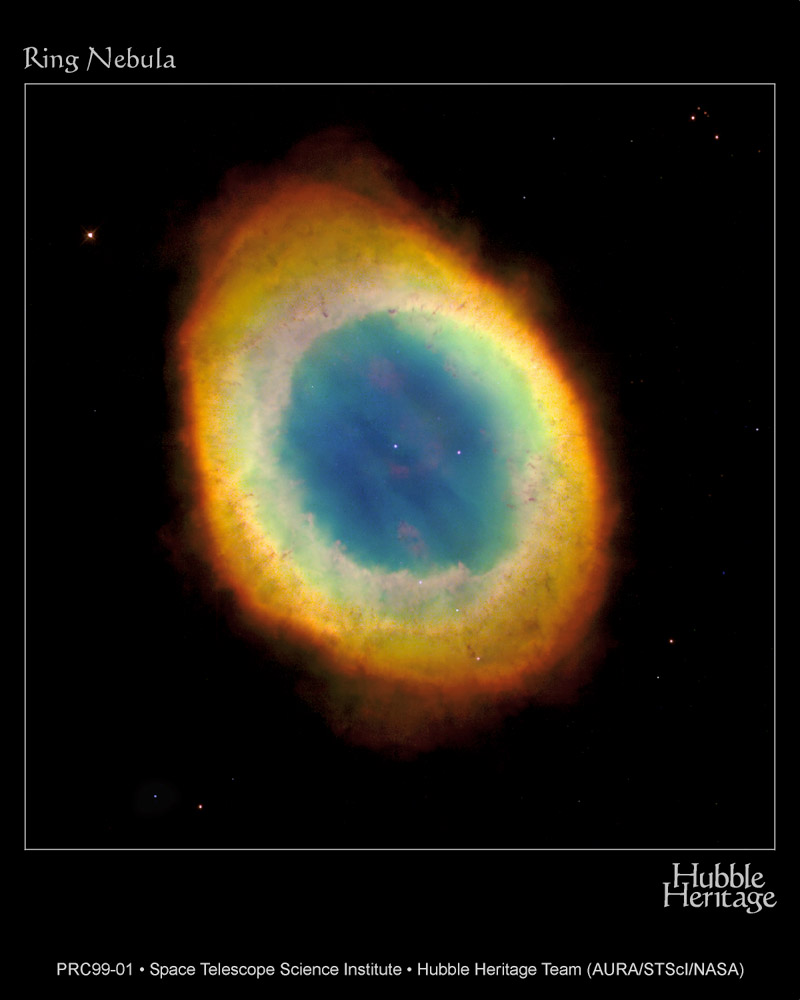
Many low-mass stars eject their outer layers before becoming white dwarfs. The result is the formation of a "Planetary Nebula", such as the Ring Nebula (above left). You will use an image of the Ring Nebula to estimate how much mass is ejected, and how long the process takes. You will also explore whether planetary nebulae replenish the interstellar dust and gas significantly.

Background and Theory

A planetary nebula is formed when a red giant star approaches the end of its life span and begins to lose a lot of mass very quickly. This mass condenses forms an expanding shell around the star. This cloud of dust and gas obscures the central star for a time. The temparature radically increases, while the luminosity remains approximately constant, and so the star moves to the left across the H-R diagram. The hotter, ultraviolet emitting layers of the star become exposed ionizing the gas in the nebula. This ionized gas begins to glow, making the nebula luminous.

Eventually, the central star becomes a white dwarf, and its luminosity falls by as much as 90%. The star is no longer capable of ionizing the nebula, so the nebula gradually fades and disperses into the interstellar medium. Planetary nebulae are responsible for a large fraction of the mass returned to the interstellar medium each year.

Planetary nebulae emit an emission line spectrum of many different colors, depending upon which atoms and ions are present. Blue-green nebulae contain OIII (oxygen ions), while red nebulae are dominated by hydrogen and nitrogen. Sometimes different regions of the nebula are different colors.

Procedure

Print out the worksheet.

Part A: Changing Mass Loss Rate

  1. Examine the images of the Ring Nebula below. The brighter regions of the image are places where the density of the nebula is high, since there is more material to create emission, or places where the material is easily ionized. Material close to the central star was probably lost recently, while material far from the star was probably lost some time ago.

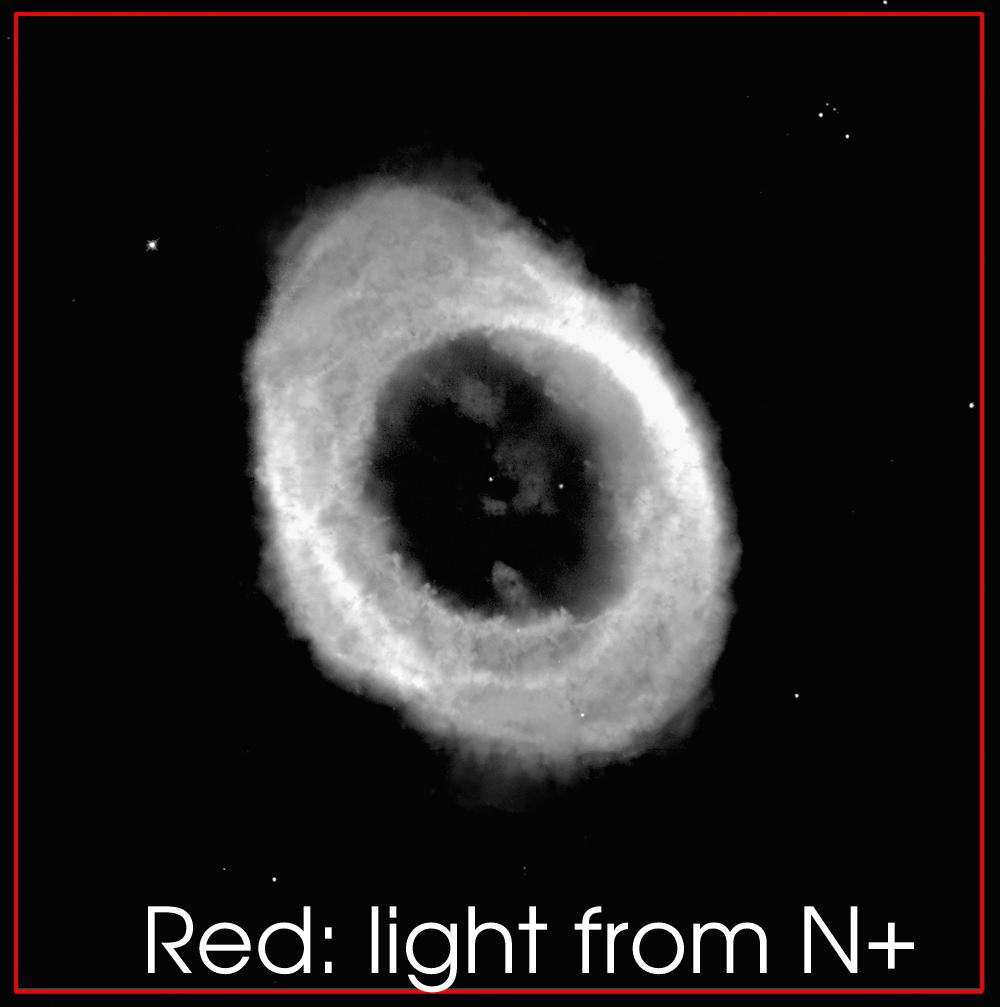
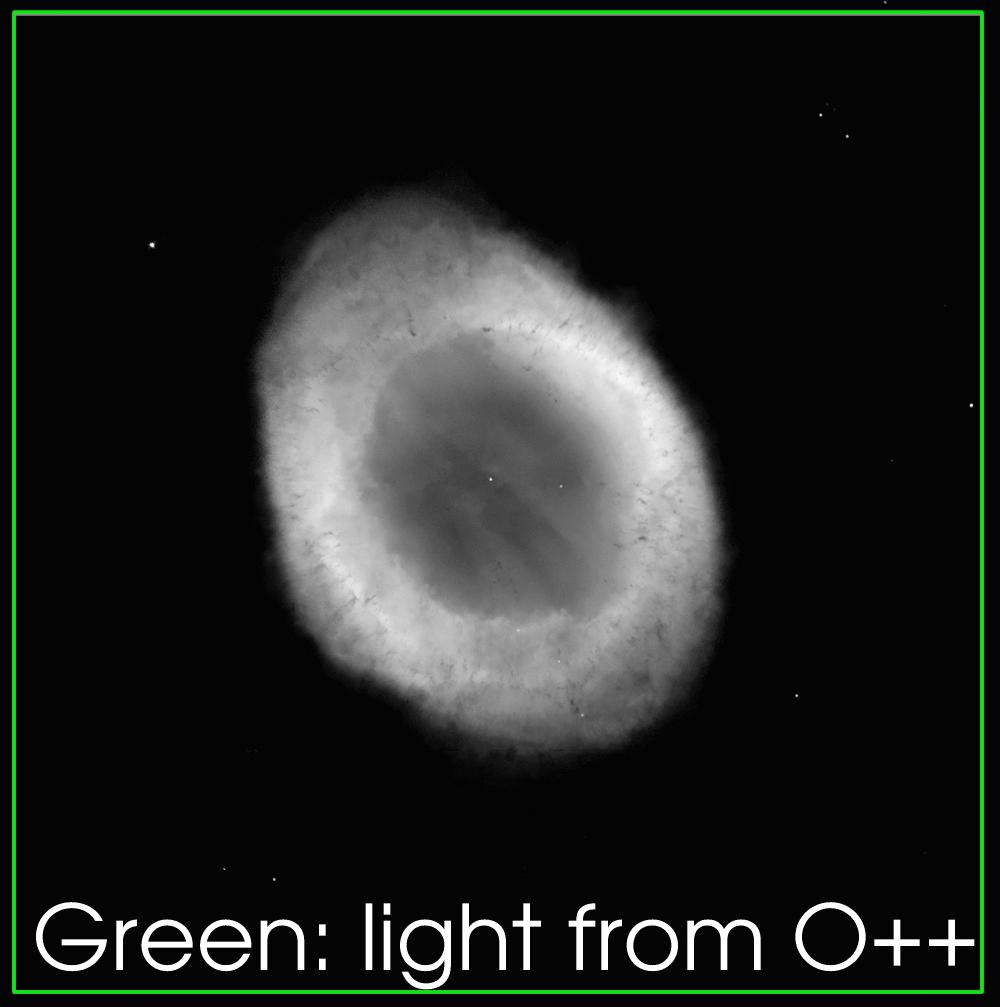
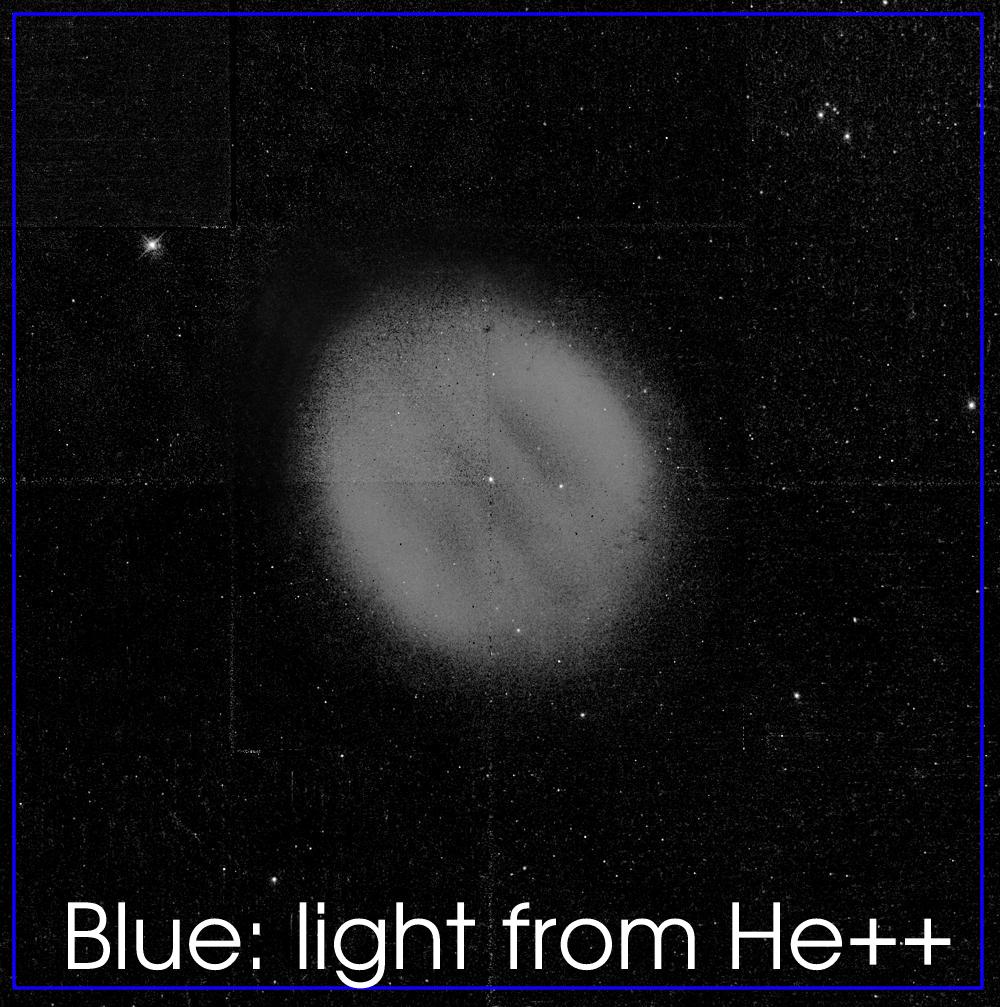    Using the O++ image, make a plot of the mass loss versus time along the long axis. Plotting the brightness of the nebula on the y-axis, and distance on the x-axis. Label your axes with arrows indicating increasing brightness, and increasing distance. Be sure to mark the position of the central star.

  2. Make the same sort of plot for the short axis. Are the two plots similar in shape?

  3. One way to interpret these data are to guess that the nebula is actually a hollow sphere. Then the middle is dim because there is less material along the line of sight, while all around the outside, the nebula is bright where you are looking through the material at the edge of the bubble.

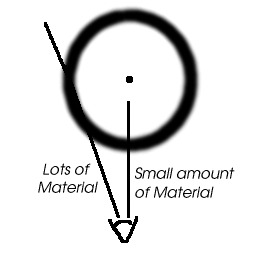    Diagram of limb-brightening of a hollow sphere.

    How do your observations differ from this model? How are they consistent?

  4. Now make a sketch of the mass loss history of the star, using the fact that material which is more distant from the central star was shed in the more distant past. This time, your plot will have time on the x-axis, and mass loss on the y-axis.

  5. Has the mass loss been constant over time? Describe the history of the mass loss from the central star.

Part B: Size and Age of the Ring Nebula
  1. Estimate the length the long axis of the nebula in the O++ image. The total image height is 2 arcminutes. Convert the answer to arcseconds.

  2. Divide this by 2 to get the radius in arcseconds. This is the angular size of the nebula, .

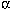  3. Now, use the small angle formula to find the actual radius, R of the nebula in kilometers. The distance, D, to the Ring Nebula is 3.4X1016 km (3,500 light years), and the small angle formula is:

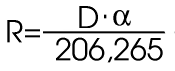
  4. We can assume that the nebula has been expanding at about 20 km/s since it first began losing mass. Given this speed, and the size of the nebula which you just found, find the age of the Ring Nebula. Don't forget to convert the age from seconds to years so that you have a sensible answer!

  5. To understand more clearly the size of the nebula, divide the length of the long axis (in km) by the distance from the Earth to the Sun (1AU = 1.5X108 km). For a sense of scale, the entire Solar System is about 80 AU across.

Part C: Mass Return Rate
  1. Use the formula for the volume of a sphere: V=(4/3)R3 to find the volume of the Ring Nebula. Use the same formula to find the volume of the hollow inner part. (You will need to find the radius of this inner part, as in steps C1-C3).

  2. Subtract the inner volume from the outer volume to find the volume that emits light. (Why?)

  3. The density of the nebula is very low, n=1.7X10-10kg/km3. Multiply this density by the volume to get the mass in the Ring Nebula in kilograms.

  4. Convert this mass to solar mass by dividing by the mass of the Sun (2X1030 kg. If the original star had a mass of one solar mass, what fraction of its mass did it eject into the nebula?

  5. The entire mass of this nebula will become a part of the interstellar medium. There are about 700 planetary nebulae in our galaxy. Estimate the mass returned to the interstellar medium each year by multiplying the mass of the Ring Nebula by the number of nebulae, and dividing by the lifetime of the Ring (in years), as found in Part B. Is this a large amount of material?

  6. New stars form at the rate of about one solar mass per year. Can planetary nebulae be solely responsible for producing the gas which is made into these new stars?

© 2003 Weber State University
Revised: 24 April, 2003