Figure 1: Radial Velocity
I. Purpose
Examine the evidence for Dark Matter in NGC 2742.
II. Background
Dark Matter is simply matter that does not interact with light. We can detect it using gravitational methods (NewtonUs Laws), but not as light. Dark Matter neither absorbs nor radiates light. We have absolutely no idea what this stuff is. Many tax dollars are being spent on physics experiments that are trying to pin down some undiscovered particle that there could be a lot of. Many astronomers are trying all sorts of clever observing schemes (if you can think of any, let us know) to find observational evidence for this stuff. As yet, every experiment and observation has come up empty.
The matter that you and I think about as being matter (atoms, protons, neutrons, buildings, whales, etc.) is sometimes referred to baryonic matter since it is made up of baryons (protons and neutrons). Baryonic matter also contains leptons (electrons), but electrons do not contribute much mass to the universe compared to the protons and neutrons. Many people believe that dark matter is non-baryonic. Physicists have a lot of fun coming up with new, imaginary particles to explain dark matter.
We will compare how much matter stars contribute to the total mass of the galaxy NGC 2742. We will discover that the total mass of a galaxy can be found by measuring how fast the galaxy rotates around its center. We will compare that total mass to the amount of light that we observe coming from the galaxy.
We want to see how much of the mass is the mass that is emitting light and how much is dark.
II. Weighing the Galaxy
Here is a graph of NGC 2742 (aka UGC 4779, galaxies get all sorts of names) that astronomers call a “rotation curve”. It plots the radial velocity (how fast stuff is moving in the line of sight direction, as shown in Figure 1) versus the radius.
Figure 1: Radial Velocity
![]()
Figure 2: Rotation Curve
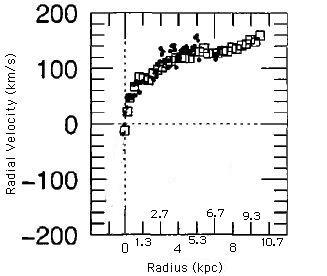
As you can see, one side of the galaxy is moving with a positive velocity (spinning away from us), while the other side has a negative velocity (spinning towards us). These data come from spectral lines that have been either blueshifted (stars moving towards us) or redshifted (stars moving away from us). Since the galaxy is tipped at an angle to us, the velocity that we detect is not the total velocity of objects orbiting around NGC 2742. Thus, a correction has been made in the above curve to take into account the inclination angle. Using Newton’s gravity equation, we will be able to determine the gravitational mass profile of the galaxy.
How did they make this?
Procedure
A. Select 7 radii all of which are to one side or the other of 0 kpc and are evenly spaced to the edge of the galaxy. Record those radii in Table 1 on the worksheet.
B. Determine the radial velocity at each of your radii. Record those values in Table 1.
C. Use your values for Radius and Velocity to determine the mass of the galaxy. Newton’s equation for gravity says:
![]() , where G = 4.31 x 10-6
, where G = 4.31 x 10-6 ![]() , and “M” is the mass contained inside of radius “R”.
, and “M” is the mass contained inside of radius “R”.
Record your results in the “Gravitational Mass” column in Table 1. Your numbers should be big. This is a galaxy you're dealing with. It contains a lot of stars.
III. How much light comes from NGC 2742?
Now that we’ve found the total mass of the galaxy, we will investigate how much of that mass comes from luminous matter like stars and gas.
Figure 3 is a graph of how many solar luminosities of light NGC 2742 produces inside of the area encompassed by some radius (where radius is the distance from the center of the galaxy measured in kpc).
Figure 3: Amount of Light Emitted from Inside some Radius
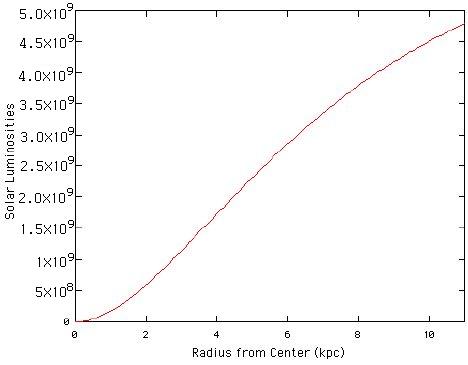
We add together all the luminosity from inside of a given radius to be consistent with the gravitational mass that we found before. The gravitational mass we calculated included all the mass inside of a spherical shell at some radius.
How did they make this?
One more note about the galaxy we selected: It is harder to figure out how much light is coming from a galaxy the more “edge-on” it is. If we are looking at the side of the galaxy, most of the light is blocked by dust. When we are looking at the galaxy “face-on” (you might think of this as from above), we see almost all the light that is coming out of a galaxy. Remember that the opposite is true for accurately determining the galaxy’s rotational velocity.
D. At the radii that you have chosen, determine a value for the luminosity of the galaxy and record it in Table 1. (The “e”s in the solar luminosity values are like the “EE” button on your calculator, NOT the “ex” button.)
Now that we've measured how much light is coming from NGC 2742, we can estimate the mass of the stuff that produced that light. We'd like to say that for every solar luminosity of light we measure we can assume that there's one solar mass of stars producing it. Unfortunately, light is blocked by dust in the galaxy we're observing, and there's a whole mix of heavy and light stars in this galaxy. Remember that luminosity is critically dependent on the mass of a star. A lot of the light we're seeing may be coming from a few young, hot bright stars that are only slightly more massive than the sun. Many cooler, low mass stars may be hidden from view by the glare of the bright stars. Thus, we need to find a compromise between the high and low mass stars. A good way of estimating the true mass of material producing the light we see is to assume that there are two solar masses of stars producing each solar luminosity of light.
E. Calculate how much mass must be present in the galaxy based on how much light we see. For every solar luminosity, count 2 solar masses and record the number in the “Radiation Mass” column of Table 1. (In other words, multiply the total luminosity by 2.) You may want to write this as a factor of 1010.
F. Plot each of the masses (gravitational and “radiation”) versus radius on the plot provided. Remember to label your axes.
G. Answer the questions on the worksheet.