THE MEANING OF ELECTRON WAVES
When electrons pass through a double slit and strike a screen behind the slits, an interference pattern of bright and dark bands is formed on the screen. This proves that electrons act like waves, at least while they are propagating (traveling) through the slits and to the screen. When an electron hits the screen, it produces a flash of light at just one place on the screen. The bright and dark bands are the result of the flashes of light produced by many electrons hitting the screen. Note that "hitting the screen" is an interaction, and the electron therefore acts like a particle with a definite position when it hits.
Recall that the bright bands in an interference pattern are found where a crest of the wave from one slit adds with a crest of the wave from the other slit. The dark bands are found where a crest of the wave from one slit cancels with a trough of a wave from the other slit. The amazing thing is that the electron wave interference pattern is formed even if only one electron at a time passes through the slit. This can only happen if each individual electron passes through both slits at the same time. After all, the wave from just one slit can't form an interference pattern since two waves are needed to add or cancel. (If an electron passing through both slits doesn't seem possible, it is probably because you are thinking of the electron as a particle. Remember, an electron behaves like a wave as it travels, and an electron wave can easily pass through both slits at the same time, just as a water wave could.)
This provides an interpretation of what the electron waves are. Each individual electron "knows" about the interference pattern, since the pattern can be built up by electrons passing one at a time through the slits. Therefore the electron wave can't tell you where an electron is, or where it will hit the screen. This is because the electron wave is spread over the entire screen (the interference pattern), while the electron itself strikes the screen and produces a flash of light at just one location. The electron wave, then, does not say where the electron will be found, only where it may be found. Electron waves (and matter waves in general) are probability waves. There is a high probability of finding the electron where the wave is large, and a small probability of finding the particle where the wave is small. (Nit-picking detail: since there can't be negative probabilities, the probability of finding the electron is actually given by the square of the size of the wave.)
The implications of this (which are described in Chapter 6 of Richard Feynman's The Character of Physical Law) are staggering. If everything in nature exhibits the wave-particle duality and is described by probability waves, then nothing in nature is absolutely certain. We can only talk about how nature will probably behave. Of course, the probability that Newton's laws will be obeyed for large objects like baseballs is very, very, very nearly a certainty. But certainty does not describe nature on a small scale, the scale of atoms, molecules, electric circuits, and neural pathways. For example, we cannot predict where a given electron will strike the screen after passing through a double slit. We can only say that there is a high probability it will strike in one of the bright bands of the interference pattern, and a low probability it will strike in one of the dark bands. Identical electrons following identical paths to the slits will hit the screen in different locations. Nature herself does not know where an electron will strike the screen before the electron actually hits.
DESCRIBING MATTER (PROBABILITY) WAVES
In 1926, Erwin Schrödinger invented a wave equation that could be applied to any physical system. The equation has more than one solution, and each solution to the Schrödinger equation is a probability wave that describes one of the possible behaviors of that system. (The technical name for one of these solutions is a quantum state. Quantum state = matter wave = probability wave; they all mean the same thing.) For example, each wave solution to the Schrödinger equation for the hydrogen atom describes one of the allowed electron orbits of the hydrogen atom. The energy and radius of each electron orbit agree with those calculated by Niels Bohr in 1913, but without using Bohr's rule. (In fact, in addition to Bohr's rule being "not too obvious," it is not correct! Bohr was lucky because the way in which his rule was wrong did not affect his values of the orbital energies and radii.) The figures on p 213/296 of Seven Ideas That Shook the Universe (1st/2nd ed) show a few of the probability wave solutions (quantum states) for the electron in the hydrogen atom. The electron will actually be found in only one of the possible quantum states. For each quantum state, you can calculate where the electron is most likely to be found. In these figures, the electron is more likely to be found where the shading is darker. In a chemistry class, you may have heard these quantum states referred to as "orbitals" or "shells."
In 1927, Paul Adrian Maurice Dirac combined the Schrödinger equation with Albert Einstein's theory of relativity to get a new equation. Like the solutions to the Schrödinger equation, the solutions to the Dirac equation are probability waves, but Dirac's waves incorporate relativity and are in better agreement with how nature behaves. For example, when applied to hydrogen and other atoms, the Dirac equation provides a more complete description and results in a complete understanding of the periodic table of the elements used by chemists.
When he applied his equation to a free electron (an electron not attached to an atom), Dirac saw that the solutions predicted the existence of antielectrons (also called positrons). A positron has the same mass as an electron, but it has a positive electric charge instead of a negative charge. Dirac's prediction was right; positrons were observed experimentally in 1932. We now know that every type of particle has a corresponding antiparticle with the opposite electric charge. When a particle and its antiparticle meet, they completely annihilate each other. They materially cancel each other out and vanish from existence. Their mass is converted into light according to E = mc2, and we see two photons flee the scene where the two particles mutually annihilated. This is called matter-antimatter annihilation.
You may wonder what sort of container you could keep a collection of positrons in. The container couldn't be made of matter, since the positrons would annihilate with the electrons in the atoms of the container. Physicists use magnetic fields to confine positrons, a sort of magnetic bottle that keeps the positrons from coming into contact with normal matter.
THE WAVE-PARTICLE DUALITY OF NATURE
What does it mean to say that an object, such as an electron or a baseball, exhibits a wave-particle duality? Waves and particles seem so different. In fact, the wave and particle characteristics of any object are complementary, in the sense that the wave and the particle characteristics are never exhibited at the same time. An object may behave like a wave or like a particle, but never both simultaneously.
Which aspect of its nature an object displays depends on the experiment that is performed. The double-slit experiment shows the wave aspect of the electron, while the photoelectric effect shows the electron's particle aspect. If an experiment is an interrogation of nature, then you get what you interrogate for. This means that there is not objective reality "out there," independent of us. The world does not unfold as a drama does on the stage, independent of the audience. Nature behaves differently depending on the questions we ask of it. We live in a participatory reality, not an objective reality from which we can separate ourselves. To observe the physical world we must interact with it, and the nature of this interaction determines how nature responds.
Let's examine an essential difference between waves and particles:
Waves are spread out, like the pure sine wave shown below.
Particles are localized; they have a definite location, like the particle shown below.

However, suppose we try adding together several pure sine waves of different wavelengths to form a resultant wave. ("Resultant" just means it is the result of adding the pure sine waves.) In some places, the crests will all add up. In other places, the crests of some of the waves will cancel the troughs of the other waves.
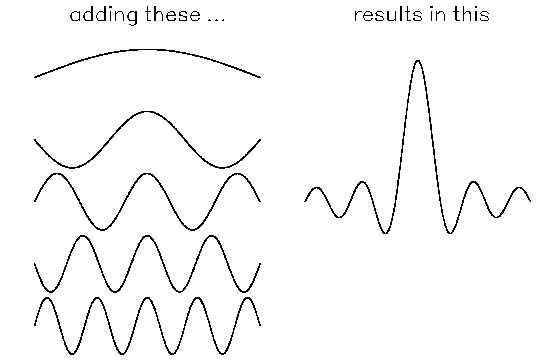
Note that the resultant wave is large only within a small region of space. In other word, adding pure sine waves of different wavelengths produces a resultant wave that is localized. The more sine waves you add together, the more the resultant wave will be localized.
Now let's ask, what is the momentum of the object that is represented by our waves? We will use de Broglie's idea that
momentum = h / wavelength
A pure sine wave has a precise wavelength, and so the object represented by a sine wave has a precise momentum. But a pure sine wave keeps going forever in both directions; it is not at all localized. Therefore we are perfectly uncertain about where the object is!
Adding together several pure sine waves with different wavelengths produces a resultant wave that is somewhat localized. The more sine waves you add together, the more the resultant wave will be localized, and the less uncertainty there will be about the object's location. However, what is the momentum of the object represented by the resultant wave? The resultant wave contains a spread of wavelengths (the wavelengths of the sine waves), and it is not clear which wavelength goes into de Broglie's formula. Thus there is some uncertainty about the object's momentum. If you add more sine waves together, the resultant wave will be more localized, but there will also be more of an uncertainty in the wavelength and momentum of the object represented by the resultant wave.
Werner Heisenberg realized that the wave-particle duality of nature implied that there was a natural tradeoff between knowing an object's position and knowing it's momentum. The greater the uncertainty in an object's particle's position, the smaller the uncertainty in its momentum. It is impossible to predict, measure, or know both the exact position of an object and its exact momentum at the same time. In fact, an object does not have an exact position and momentum at the same time! This is called the Heisenberg uncertainty principle, and it is a natural consequence of the wave-particle duality of nature. Recalling that a particle's momentum is just its (mass) x (velocity), Heisenberg's uncertainty principle says that an object does not have an exact position and velocity at the same time.
This deals a fatal blow to the Newtonian clockwork universe. The idea of a deterministic universe was that if we could know the exact position and velocity of every atom in the universe, then the entire history of the universe could be calculated, at least in principle. Heisenberg's principle demolishes that idea, because nothing in the universe has an exact position and an exact velocity. The future is not determined, not in fact and not in principle. Nature simply does not know how the future will unfold.
Quantum physics does not explain our human free will, but it does free us from the shackles of a deterministic universe. Today's electronics uses the Heisenberg uncertainty principle in certain devices; it is not unreasonable to believe that it must also affect neural pathways in the brain. Modern physics shows that the brain is not deterministic; our future thoughts are not determined by our past thoughts or by our environment. But modern physics cannot even begin to explain how Shakespeare wrote Hamlet, or how Stoppard wrote Arcadia. Free will remains a profound mystery.
Return to Honors PS1500 home page
Last modified: Monday, January 24, 2005 11:02 AM