This introduction to special relativity is for anyone who is already comfortable with the Newtonian concepts of velocity, acceleration, momentum, and energy. It is intended as a compromise between the extremely rushed treatments of relativity that appear in standard introductory physics textbooks, and the more leisurely treatments that appear in books dedicated to teaching just relativity. I’ve tried to emphasize depth more than breadth, addressing the most important conceptual issues and introducing the conceptual tools (including spacetime diagrams) that show how the theory fits together.
In my own introductory physics course I deliver these five lessons during five 50-minute class sessions, and we spend two more class sessions discussing the assigned homework problems. This is nearly double the class time for relativity that a traditional introductory course would allocate, but in my mind it’s the absolute minimum.
In preparing these lessons I’ve drawn heavily on the treatments in the three special relativity texts listed at the end under Further Reading. Many thanks to authors William L. Burke, Peter Scott, Thomas A. Moore, Edwin F. Taylor, and John A. Wheeler!
“Relativity” is short for what Albert Einstein called his “special theory of relativity”, published in 1905. This “theory” is a revised framework for the laws of mechanics. It tells us that Newton’s laws of motion are only approximate, and become especially inaccurate when we apply them to objects that move extremely fast. Relativity replaces Newton’s laws, and the related principles of momentum and energy conservation, with new versions that are accurate at all speeds. (Ten years later Einstein published what he called his general theory of relativity, which is actually a revised theory of gravity. That theory is beyond the scope of these brief lessons.)
The mathematics of special relativity is no more difficult than that of Newtonian mechanics: basic algebra and calculus, using derivatives to define velocity and acceleration. The main difference you’ll notice is that a lot of the formulas now involve square roots.
What makes relativity difficult to learn is not the mathematics, but the concepts. You see, the problem with Newton’s laws isn’t merely that the equations aren’t quite right; it’s that the underlying concepts turn out to be inadequate. In particular, Newtonian mechanics rests on an oversimplified conception of time. Unlearning the Newtonian concept of time and replacing it with the far richer version in relativity theory can be quite a challenge. In order to master relativity, you’ll need to take on this challenge and wrestle with the concepts until they fall into place.
Another thing you should know about special relativity is that it doesn’t have many direct practical applications. You’ll need it if you ever write software for satellite-based navigation systems (GPS and similar), which require super-accurate timing on satellites orbiting at thousands of miles per hour. And it’s fundamental to understanding a lot of astrophysics and nuclear physics and elementary particle physics. But in everyday life its role is mostly hidden. So you might wonder whether you really need to know relativity. Why should you put in the effort to learn an esoteric branch of physics you may never use?
The short answer is that relativity is just too much fun to skip over. But a more serious version of this answer is that special relativity is the best subject I know for teaching us to think in new ways. It forces us to jettison our preconceptions about time and velocity and mass. Doing that takes courage. But in return for taking that brave step, relativity rewards us with a universe that is strikingly beautiful and far more fantastic than anything a science fiction writer could have invented. This process of opening ourselves to new ideas is the essence of science, and the essence of learning. How could we possibly pass up such an opportunity?
So where do we start? With the concept of a reference frame.
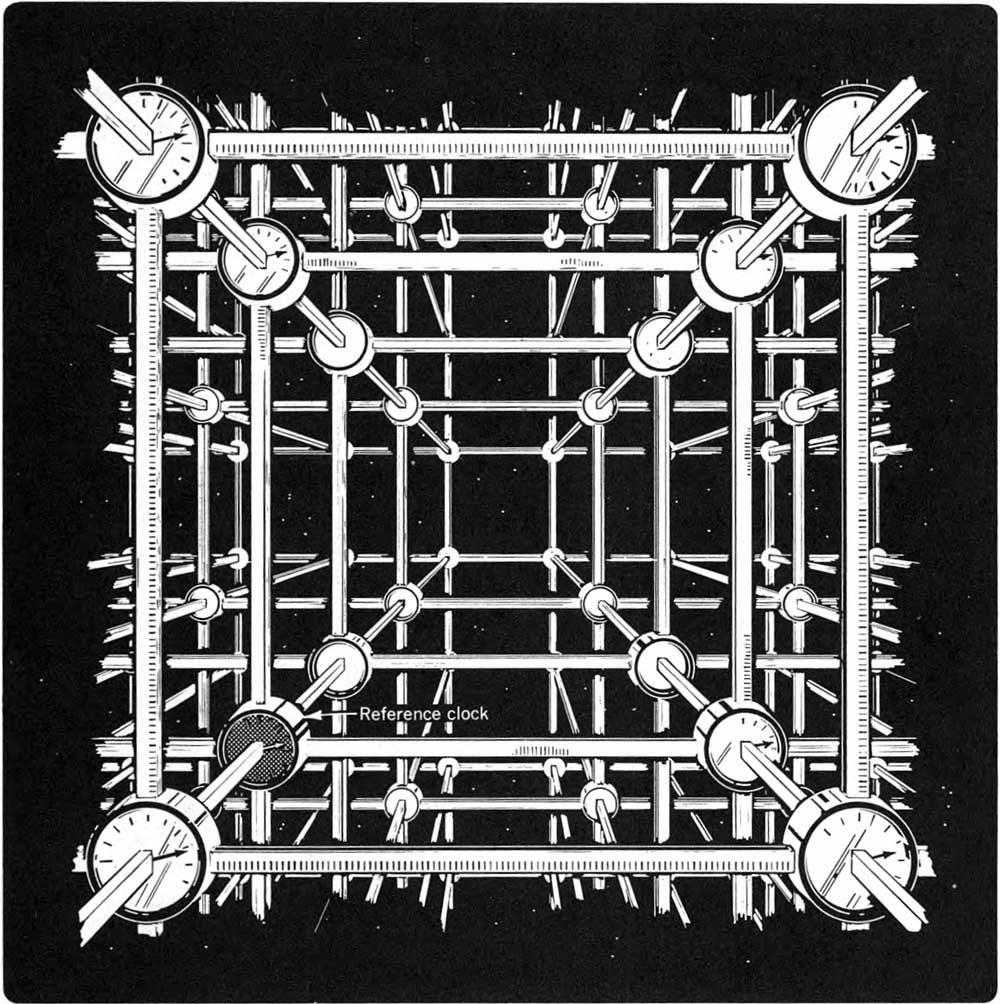
I hope you recall something about reference frames from your study of Newtonian physics. Basically a reference frame is a coordinate system: $x$, $y$, and $z$ axes, laid out with respect with some origin, along with a consistent method of measuring time. You can picture a reference frame as a three-dimensional lattice of meter sticks, with a clock located at each lattice point, as in this vivid illustration from the book Spacetime Physics:

Using this structure we can measure both the location and the time of any localized event, such as the collision of two billiard balls or the flashing of a strobe light. In practice we never actually set up such a cumbersome structure, but we need to remember that whatever method we do use to measure locations and times of events must be equivalent to this one, in the sense that it yields all the same numbers for position and time measurements. (Also, in practice, we can often get by with system for measuring positions and times in just a two-dimensional plane, or even just along a one-dimensional line, where our events of interest take place.)
When we set up a reference frame, we must make several arbitrary choices: the location of the origin (labeled the “reference clock” in the above illustration), the orientations of the three spatial axes, the origin of time (when the clocks read zero), and, crucially, the state of motion of our reference frame. Different choices will give us different measurements for the $x$, $y$, $z$, and $t$ coordinates of any given event, so we say that these positions and times are relative.
If you’re not yet completely comfortable with the concept of a reference frame and the idea that measured quantities can be relative, I highly recommend this classic film on the subject:
My reference frame has its origin at the post office, $x$ axis pointing east, $y$ axis pointing north, and $t=0$ at high noon. Your reference frame has its origin at the library (5 blocks due east from the post office), $x$ axis pointing north, $y$ axis pointing west, and $t=0$ at 9:00 a.m. (when the library opens). Suddenly, a door slams (Event S). Some time later, a dog barks (Event B). Using my reference frame, I determine that the coordinates of Event S are $x=3$ blocks, $y=2$ blocks, $t=1$ hour, while the coordinates of Event B are $x=-1$ block, $y=-3$ blocks, $t=3$ hours. (a) What coordinates do you measure for these events? (b) Use my $x$ and $y$ coordinates and the Pythagorean theorem to calculate the distance between them (just in space, ignoring time). Then calculate the distance again using your coordinates, and comment on the result.
Not everything is relative! Even though position and time measurements are relative to our choice of reference frame, the laws of physics themselves are absolute! More precisely, the laws of physics are the same from the perspective of every inertial reference frame, that is, every frame in which the law of inertia holds. (Inertial reference frames can move with respect to each other slowly or rapidly, in any direction, so long as they do not accelerate.) This fact of nature is called the principle of relativity:
The laws of physics are the same in every inertial reference frame.
– or –
All inertial reference frames are equally valid, so there’s no physical experiment that can determine who is “really” moving.
This principle dates back 400 years, to the time of Galileo. It is built into Newton’s laws of motion, which say that forces cause changes in an object’s motion, but do not cause motion itself.
Imagine a tennis ball as it is slapped back and forth across the court, with a highly variable velocity $\vec u(t)$. At every instant the ball’s acceleration $d\vec u/dt$, with respect to a reference frame anchored to the ground, is determined by the various forces $\vec F$ exerted on it (by the rackets, the ground surface, the air, and Planet Earth), according to Newton’s second law: $d\vec u/dt = (\sum\vec F)/m$, where $m$ is the ball’s mass. Now imagine watching the game from a bicycle that’s coasting alongside the court at constant velocity $\vec v$. According to the Galilean velocity transformation law, you measure the ball’s velocity at any instant to be $\vec u' = \vec u - \vec v$. (For example, if your speed is 3 m/s and at a certain instant the ball is moving parallel to you at 10 m/s with respect to the ground, then you measure its speed to be 7 m/s. We’ll see in Lesson 4 that this transformation law is not quite correct, but please assume for now that it is.) Assuming that the forces and mass are the same in all frames of reference, prove that Newton’s second law holds true in your frame of reference as well. Also explain why your proof would not apply if your bicycle were accelerating.
A 1-kg block glides in the $x$ direction at 10 m/s on frictionless ice until it collides with a second 1-kg block, initially at rest. The two blocks stick together (there’s Velcro on them) and continue gliding in the $x$ direction. (a) What is the initial momentum of the two-block system? (b) Using the ordinary Newtonian law of momentum conservation, predict the final velocity of the two combined blocks. (c) Now imagine viewing this collision from a reference frame that is moving (with respect to the ground) in the $x$ direction at 5 m/s. Use the ordinary Galilean velocity transformation law (see the previous exercise) to determine the initial velocities of both blocks in this frame, as well as their joint final velocity. (d) Use the results of part (c) to calculate the system’s initial and final momentum in the new reference frame. Is momentum the same in all frames of reference? Is the law of momentum conservation consistent with the principle of relativity? Explain briefly.
But by the late 1800s, physicists had convinced themselves that the principle of relativity does not apply to the laws of electromagnetism. That’s because Maxwell’s equations for the electric and magnetic fields predict that electromagnetic waves (including visible light) travel at a speed of
\begin{equation} \frac1{\sqrt{\epsilon_0\mu_0}} = c = 3.00\times10^8~\textrm{m/s}. \end{equation}Question: 300 million meters per second with respect to what? Between 1865 and 1905, everyone assumed the answer was: with respect to some preferred frame of reference, in which the (hypothetical) medium that transmits electromagnetic waves (then called the ether) is at rest.
But Einstein wasn’t so sure. He was familiar with a common demonstration that you may have seen, in which we move a coil of wire relative to a magnet, inducing a current measured by a galvanometer:
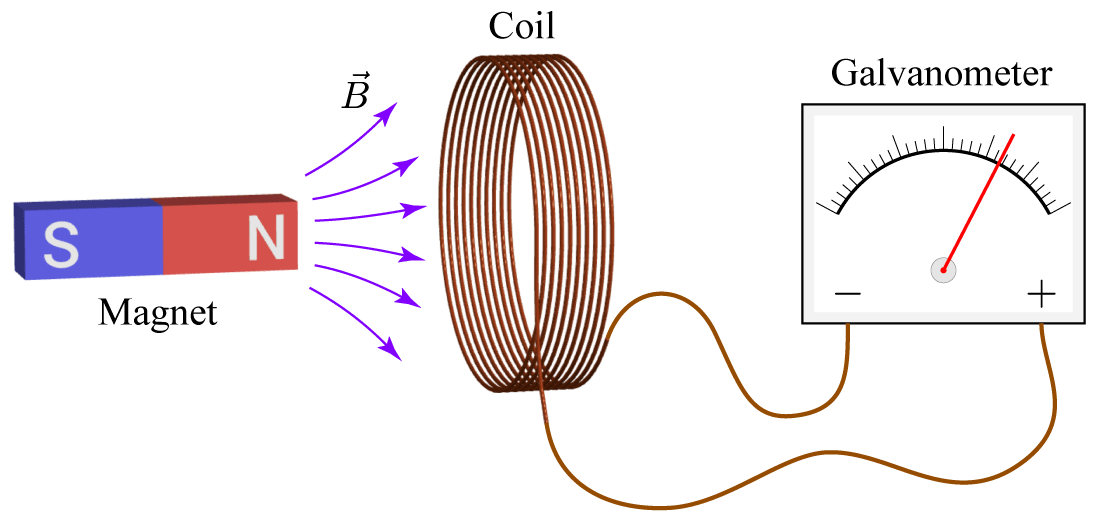
When we do this we get the same deflection of the needle regardless of whether we move the coil with the magnet fixed or move the magnet with the coil fixed. And yet we explain those two scenarios in completely different ways! When the coil moves, we say the moving electrons feel a magnetic force ($q\vec v\times\vec B$) that makes them circulate around the coil. On the other hand, when the magnet moves (and the coil is fixed), we know the stationary electrons can’t feel any magnetic force (since $\vec v = 0$), but they do feel an electric force from the circulating electric field $\vec E$ that’s temporarily created by the changing magnetic field according to Faraday’s law.
Einstein said this can’t be a coincidence. Somehow, despite these differing explanations, the laws of electromagnetism must fundamentally respect the principle of relativity, so they predict the same phenomena regardless of whether we view things from the reference frame of the magnet or the reference frame of the coil. (Einstein’s 1905 paper begins with exactly this example; you can read an English translation of it here or here.)
But then what about the speed of light? If the laws of electromagnetism are equally valid in all inertial frames of reference, and if those laws predict that light travels at 300 million meters per second, then light must travel at that speed with respect to every inertial frame of reference—despite the fact that one reference frame could be moving with respect to another at (say) half the speed of light or faster! That seems impossible, but in fact it’s not. It’s just contrary to the intuition that we’ve developed by watching slow-moving objects.
The price we pay for accepting this seemingly impossible fact about light is that we must discard some of our assumptions about time. We use time to define speed, so perhaps if time is sufficiently screwy, speeds might also defy our intuition.
(Electromagnetism review.) In the illustration above of the magnet and coil, the rightward swing of the galvanometer needle away from vertical indicates that a positive current is flowing into the terminal marked +. Look at the direction in which the coil is wound, then answer the following: (a) First assume that the magnet is fixed and the coil is moving horizontally, along its axis. Use $\vec F=q\vec v\times\vec B$ and the right-hand rule for cross-products to determine whether the coil is moving toward or away from the magnet. Which component of the magnetic field—rightward along the axis or outward away from the axis—causes the current to flow? (b) Now assume instead that the coil is fixed and the magnet is moving horizontally. Use Faraday’s law (or Lenz’s law) to explain which direction the magnet must move to give a positive current as shown.
Recall the picture of a reference frame above, with a clock at every grid location. To measure the time when an event occurs, we look at the reading of whatever clock lies nearest to the event. But to compare the times of events that happen in different places, we need to make sure our clocks are all synchronized with each other. How do we do that?
You might think we could pick up our reference clock and carry it sequentially to the locations of all the other clocks, setting each of them to match it. As we’ll later see, that method won’t work: accelerating the reference clock into motion, then stopping it when it arrives near some other clock, will affect its measurements. (You don’t need to actually believe this yet—just accept that the accelerations could affect the measurements, and agree not to use this method of clock synchronization.) Fortunately, there’s a much better way to synchronize the clocks: Just look at them! But when you do, be sure to take into account that the light from different clocks might have taken different amounts of time to reach you. If you’re the same distance from two different clocks (as measured by all those meter sticks!), then you should always see them reading the same time. If you’re looking at a clock that’s one light-second away (300 million meters, or about 3/4 the distance to the moon), then you should see it running exactly one second behind the clock at your location, because the light from the distant clock took that long to reach you. Because the speed of light is the same with respect to all inertial reference frames (and doesn’t depend on the direction the light travels), we can be confident that this light-travel-time adjustment will always work as expected.
Suppose you’re standing still (with respect to the ground) and looking at a clock tower 200 meters away. If your wristwatch reads exactly 8:18 a.m. and the clock on the tower is perfectly synchronized with it, what time should you see on the tower’s clock face?
Now that we know how to synchronize our clocks, I’m ready to carefully define time. Specifically, I want to define the time between two given events, each of which is localized in both time and space. For instance, Event A might be the lighting of the fuse on a firecracker, while Event B might be the explosion of the firecracker, some time later. How should we define the time interval between Event A and Event B? There are actually three conceptually distinct ways we can do it:
You run a single lap around a track, while your coach, standing at your starting (and ending) location, times your lap with a stopwatch. Event A is the start of your lap while Event B is the finish. What kind(s) of time between these events is/are measured by the stopwatch? What kind(s) of time between these events is/are measured by your wristwatch? Explain carefully.
You are standing near a railroad track when a train rushes past you, moving at constant velocity. Let Event A be the locomotive (at the front of the train) passing you, and let Event B be the caboose (at the rear of the train) passing you. You measure the time between these events with your wristwatch, while the train’s engineer (in the locomotive) and conductor (in the caboose) measure the time between these events using their pocket watches, which they have carefully synchronized. What kind of time do you measure between the two events? What kind of time does the train’s crew measure?
To visualize the times and locations of various events, I now want to introduce a tool called a spacetime diagram. It’s really just a plot of one-dimensional position (x) and coordinate time (t), like we use for one-dimensional motion when studying basic kinematics. But there are two new twists: First, it’s conventional to plot x horizontally and t vertically. This reversal may seem strange at first, but I think you’ll soon get used to it. Second, we space the tick marks equally along both axes, such that our unit of distance is whatever distance light travels in one unit of time. For instance, you’ve probably heard of measuring distances between stars in light-years, where a light-year is the distance that light travels in one year (nearly $10^{16}$ meters); this will be our unit of distance if we measure time in years. If instead we measure time in seconds, then our distance unit is one light-second, or 300 million meters (about 3/4 of the distance to the moon). Or, for events occurring in a smaller laboratory, we can measure time in nanoseconds and distance in light-nanoseconds (one light-nanosecond is 0.3 meters, or about a foot). The slow-moving objects we’re used to don’t travel very far in a nanosecond, and would take a long time to travel a light-second, let alone a light-year. But for the fast-moving objects that make relativistic effects apparent, these unit choices will be very convenient.
Here is a spacetime diagram, calibrated in seconds and light-seconds, on which I’ve plotted several events:
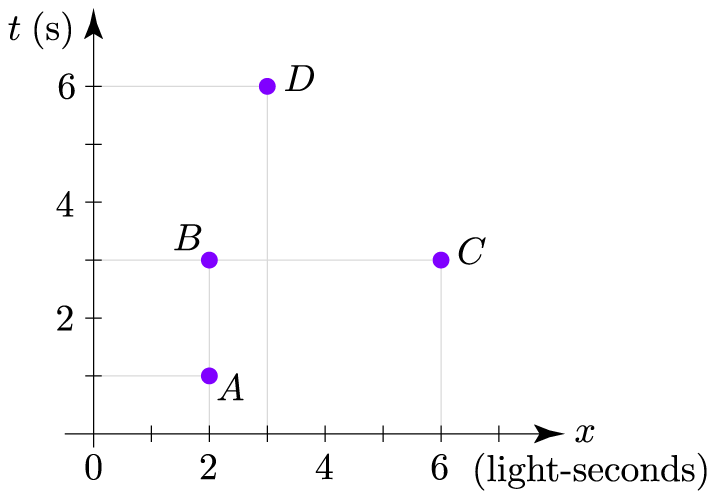
Notice that an event, localized in both space and time, is represented on the diagram by a point. We plot each point on the diagram according to its coordinates $(x,t)$ in some particular inertial reference frame; if we used a different inertial frame then the appearance of the diagram would change (as we’ll see in detail in Lesson 4). But at least from the perspective of this inertial reference frame, the diagram shows us at a glance that Event A (starship’s warning sirens sound) occurs at $t=1$ second and $x=2$ light-seconds; that Event B (deflector shields are raised) occurs at the same place, two seconds later; that Event C (enemy ship fires photon torpedoes) occurs at the same time as B, four light-seconds away to our right; and that Event D (science officer raises eyebrow) occurs three seconds later still and at $x=3$ light-seconds.
Now think about a sequence of events that all happen to a particular object: perhaps the flashes of a strobe light, or the beats of a person’s heart. If we plot these events on a spacetime diagram and connect the dots together, we have a record of that object’s (or person’s) motion:
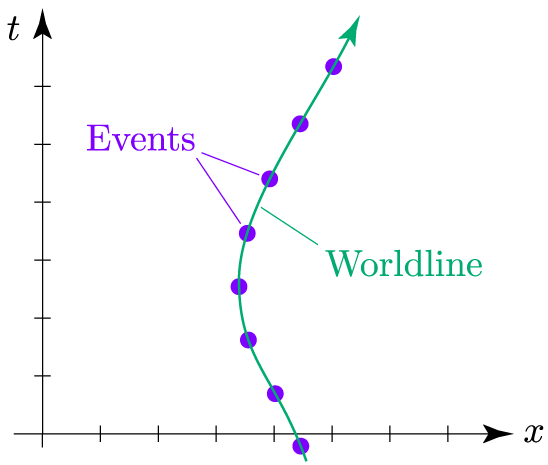
We refer to the line or curve connecting all events that happen to a particular object as that object’s worldline—its line through the “world” of space and time. Often we draw an upward-pointing arrow on a worldline, to remind us that the object’s history flows from bottom to top.
Here are some more worldlines:
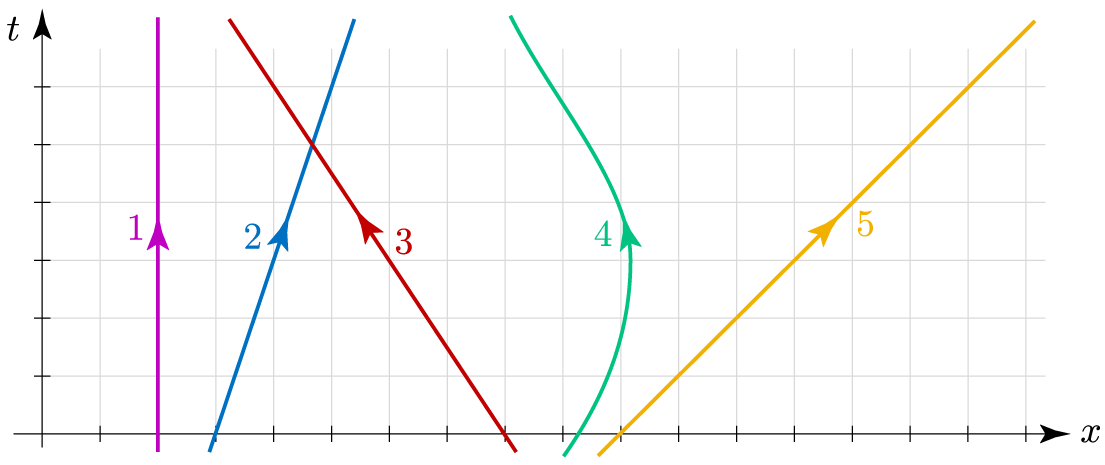
Object 1 is at rest, always at the same $x$ value. Object 2 is moving to the right at a constant velocity of 1/3 the speed of light (one light-second of distance in each three seconds of time), while object 3 is moving to the left (in the $-x$ direction) at 2/3 the speed of light. Notice that the faster an object’s motion, the shallower the slope of its worldline. Object 4 is initially moving to the right but then slows down, stops, and gradually begins moving to the left. Object 5 is a light pulse, moving rightward at the speed of light: one light-second per second. A light pulse worldline always lies at a 45-degree angle on a conventionally calibrated spacetime diagram.
Again, each of these spacetime diagrams is plotted from the viewpoint of one particular inertial reference frame; let’s call it the Home Frame. If instead you measure events with respect to some Other Frame that’s moving to the right at 1/3 the speed of light (with respect to the Home Frame), then your spacetime diagram will show Object 2 at rest, with a vertical worldline, and Object 1 moving to the left at 1/3 the speed of light. Motion is relative! Lesson 4 explains in detail how to translate a spacetime diagram from one inertial reference frame to another.
For a delightful animated explanation of reference frames and spacetime diagrams, I recommend the Minute Physics video Spacetime Diagrams. The video even shows how to add a $y$ axis to a spacetime diagram, to depict motion in two spatial dimensions. But it doesn’t use the convention of calibrating the space and time axes so that light signal worldlines are always at 45 degrees.
At $t=0$ an uncrewed rocket is launched from earth, traveling in the $+x$ direction at 4/5 the speed of light (with respect to earth). After 10 seconds, as measured in earth’s frame of reference, the rocket explodes. A burst of light from the explosion travels back toward earth, where authorities detect the light some time later. Draw a calibrated spacetime diagram that accurately shows these objects and events, as observed in earth’s reference frame. Label the launch event, the explosion event, and the detection-of-light event, as well as the worldlines of earth, the rocket, and the light burst.
Look again at the spacetime diagram above with events labeled A through D. This diagram is drawn from the perspective of some Home reference frame. What velocity would some Other reference frame need to have, with respect to the Home frame, in order for observers in the Other frame to observe Event B and Event D to occur at the same place? Explain carefully.
In the previous lesson I defined three different ways of measuring the time between any two events: coordinate time, proper time, and the spacetime interval. My goal for this lesson is to show you how the coordinate time between two events, in any inertial reference frame, is related to the spacetime interval between those events. (I’ll discuss the proper time measured by an accelerated clock in the following lesson.) To show this relationship from different perspectives I’ll describe three experiments:
Experiments 1 and 3 are mere thought experiments, which would be impractical to carry out in the way I’ll describe. Experiment 2 is a real experiment that has actually been performed.
Imagine that I have a fistful of firecrackers, all with identical 10-second fuses. (I know the fuses are identical, and absolutely reliable, because they come from the world’s most reputable firecracker factory, and because I’ve already tested many randomly chosen firecrackers from the same batch and found all their fuses to burn for exactly 10 seconds.) I’m standing with my firecrackers at the origin ($x=0$) of an inertial reference frame, with a long measuring tape stretched out in both directions along my $x$ axis, and an array of carefully synchronized clocks located along the measuring tape at short intervals.
At $t=0$ I use a match to light the fuses on all the firecrackers, and simultaneously hurl them in both directions, at an assortment of speeds. Some go fast, while others go slow. Some go in the $+x$ direction, while others go in the $-x$ direction. I give one of the firecrackers a velocity of zero, holding it in my hand for reference.
Eventually all the firecrackers explode, and I carefully record the places and times of these explosions. How do I do that? I could station an assistant at each clock, with instructions to record the location and clock reading when an arriving firecracker explodes. Or I could just watch for the explosions, using binoculars to view the tape label and clock reading at each explosion event. Of course the light from these explosions will take time to reach me, and that delay will be longer for the more distant explosion events, so I don’t expect to actually see all the explosions at the same time. But if I didn’t know anything about special relativity, I would still expect all the explosion events to occur at the same time. Plotted on a spacetime diagram, the explosion events should (I expect) all lie on a horizontal line:
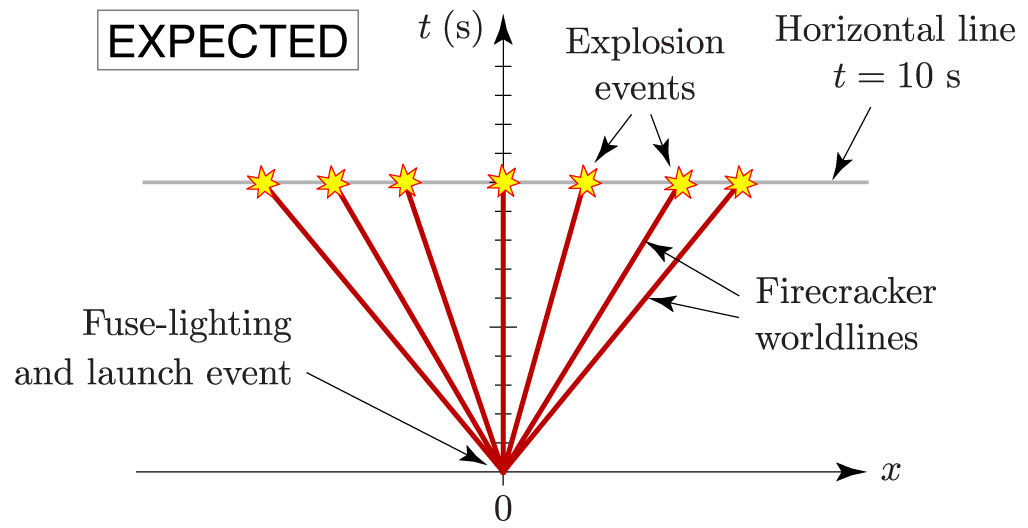
On this diagram my own worldline coincides with the $t$ axis, because I’m at $x=0$ and not moving (with respect to my own reference frame). The vertical red line is the worldline of the firecracker that I’m holding in my hand, and its explosion event is plotted at $x=0$ and $t=10$ seconds. I expect all the other explosion events to also occur at $t=10$ seconds, as shown.
But that’s not what actually happens.
The firecracker that I’m holding in my hand really does explode at $t=10$ seconds, as expected. But the other firecrackers explode later than $t=10$ seconds, by an amount that’s tiny if they’re moving slowly but that grows quite large if they’re moving at nearly the speed of light (with respect to my reference frame). Plotted on a spacetime diagram, the explosion events actually lie on a hyperbola that’s defined by the formula $t=\sqrt{(10~\textrm{s})^2+x^2}$ (with the understanding that $x$ is measured in light-seconds):
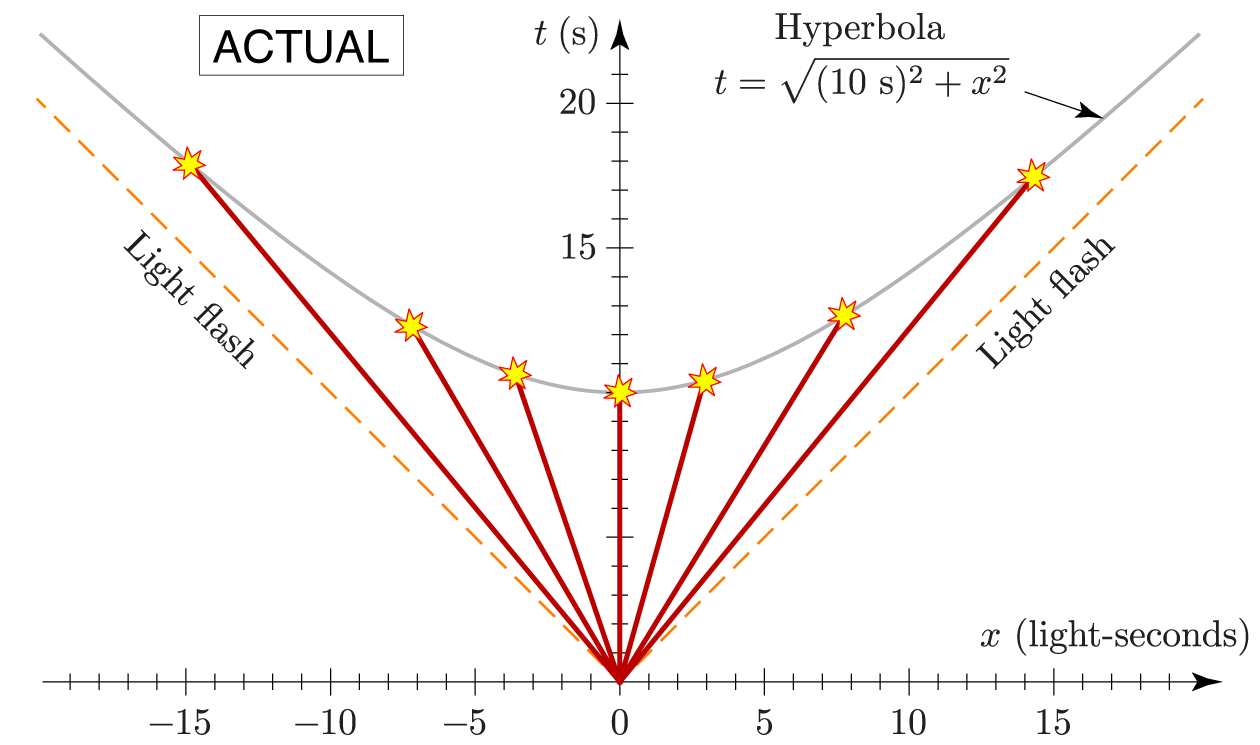
As you can see, the hyperbola is quite flat near the middle of the diagram, so for slow-moving firecrackers we could easily mistake it for a horizontal line. Meanwhile, the explosion events for fast-moving firecrackers can occur at arbitrarily large distances (in either direction), and at arbitrarily late times, because the hyperbola extends infinitely far in both directions, asymptotically approaching the 45-degree worldlines of the light flashes traveling outward from the match that I used to light the fuses.
Does this shocking result mean that something was wrong with those firecracker fuses after all? No! Each fuse truly measures exactly 10 seconds between the fuse-lighting event (call it Event A) and the explosion event (call it Event B). But there’s no logical necessity to our expectation that the time between these two events as measured by the fuse must be the same as the time between them as recorded in my inertial reference frame (and plotted on my $t$ axis). For the fuse, which is present at both events and doesn’t accelerate along the way, measures the spacetime interval $\Delta s_{AB}$ between the fuse-lighting event A and the explosion event B, whereas the clocks in my inertial reference frame, no one of which is present at both events, instead measure coordinate time $\Delta t_{AB}$.
The mathematical relationship between coordinate time and the spacetime interval is summarized in the equation for the hyperbola given above. For an arbitrary pair of events A and B, the equation reads
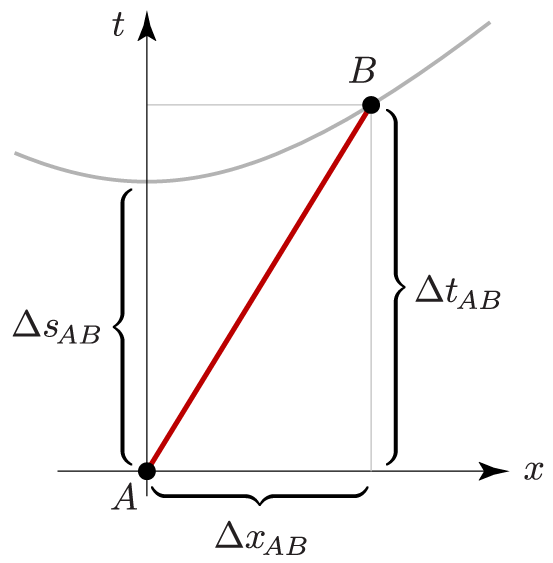
\begin{equation} \Delta t_{AB} = \sqrt{(\Delta s_{AB})^2 + (\Delta x_{AB})^2}, \end{equation}where $\Delta s_{AB} = $ 10 seconds in the firecracker example, and again with the understanding that $\Delta x_{AB}$ is measured in units of the distance that light travels in one time unit (e.g., light-seconds if the times are in seconds). This relationship is called the metric equation of special relativity, and is summarized in this simple spacetime diagram:
We can write the metric equation in many other ways. For instance, if we square both sides and move the $\Delta x$ term to the left, we obtain
\begin{equation} (\Delta t_{AB})^2 - (\Delta x_{AB})^2 = (\Delta s_{AB})^2. \end{equation}I like this version because it puts the frame-dependent coordinate differences (which of course must be measured in the same reference frame) on one side and the unique spacetime interval on the other. There is a deep analogy between the metric equation and the Pythagorean formula for calculating distances in a two-dimensional plane—but the metric equation has a minus sign where the Pythagorean formula has a plus.
If you’d rather measure $\Delta x$ in more conventional units, then the $\Delta x$ term in the metric equation requires a conversion factor. For instance, if $\Delta x$ is in meters and the times are in seconds, then to convert $\Delta x$ to light-seconds we divide by the number of meters in a light-second, $3\times10^8$. More generally, to convert $\Delta x$ to appropriate light-travel units we must divide by the speed of light:
\begin{equation} (\Delta t_{AB})^2 - \Bigl(\frac{\Delta x_{AB}}{c}\Bigr)^2 = (\Delta s_{AB})^2. \end{equation}Yet another variation is to notice that $\Delta x/\Delta t$ is the velocity of the clock (e.g., a firecracker’s fuse) that measures $\Delta s$, with respect to our inertial reference frame. Denoting this velocity $v$, we can then insert $\Delta x = v\,\Delta t$ to write the metric equation in terms of $v$ instead of $\Delta x$:
\begin{equation} (\Delta t_{AB})^2\Bigl(1-\frac{v^2}{c^2}\Bigr) = (\Delta s_{AB})^2, \quad \textrm{or}\quad \Delta t_{AB} = \frac{\Delta s_{AB}}{\sqrt{1-(v/c)^2}}. \end{equation}This is the form of the metric equation that’s most often written in introductory textbooks, although these books usually call it the “time dilation equation”, and instead of $\Delta s$ they often use the notation $\Delta \tau$ or $\Delta t'$.
I’ve been assuming that we orient our reference frame’s $x$ axis so Events A and B are separated only in the $x$ direction, not $y$ or $z$. To drop this assumption, just replace $(\Delta x)^2$ in the metric equation with the square of the spatial distance between the events, $(\Delta x)^2+(\Delta y)^2 + (\Delta z)^2$. When we write the metric equation in terms of $v$ instead of $\Delta x$, that means $v^2 = v_x^2+v_y^2+v_z^2$.
When applying the metric equation, the most common difficulty is figuring out whose clocks measure $\Delta t$ and whose clock measures $\Delta s$. I find it helpful to keep referring back to the last figure above, which shows that $\Delta t$ is always longer than $\Delta s$, and that $\Delta s$ is the time interval as measured by the unique, nonaccelerated clock that is present at both events.
Suppose that one particular firecracker, among those described above, has a velocity (with respect to your reference frame) of 2/3 the speed of light. What are the $x$ and $t$ coordinates of its explosion event? At what time do you (standing at the origin) see the light from this explosion? Draw and label a spacetime diagram to illustrate your answers.
Suppose that one particular firecracker, among those described above, explodes at $x=-12$ light-seconds. What is the coordinate time of this explosion event? What is this firecracker’s velocity? At what time do you (standing at the origin) see the light from this explosion? Draw and label a spacetime diagram to illustrate your answers.
Suppose that one particular firecracker, among those described above, has a velocity (with respect to your reference frame) of 200 kilometers per second (slightly faster than NASA’s fastest-ever space probe). What are the $x$ and $t$ coordinates of its explosion event?
For the events A, B, C, and D shown in the first spacetime diagram in the previous lesson, use the metric equation to calculate the spacetime intervals $\Delta s_{AB}$, $\Delta s_{BD}$, $\Delta s_{AD}$, and $\Delta s_{CD}$. How does $\Delta s_{AD}$ compare to the sum $\Delta s_{AB} + \Delta s_{BD}$? What happens if you try to calculate $\Delta s_{AC}$ or $\Delta s_{BC}$? Can you generalize your answers to these questions?
You wish to travel to the Vega star system, 25 light-years from earth. Being impatient, you would rather not spend more than 15 years of your own time on the journey. How fast must your spaceship travel? How long does your trip take, according to observers on earth (or on Vega, which is more or less at rest with respect to earth)? Draw an accurate spacetime diagram showing the worldlines of earth, Vega, and your spaceship.
Repeat the previous exercise for a trip to Polaris (the North Star), which is 430 light-years distant. Assume again that the trip should take no more than 15 years of your own time. Sketch a spacetime diagram to convey the idea of your calculation, but don’t worry about making it quantitatively accurate (which would be difficult). Is there any limit to how far out into the universe you can travel within a human lifetime?
People often describe the metric equation with the ambiguous phrase moving clocks run slow. Explain why this phrase can be misleading, and give an example in which it is the “stationary” clock that “runs slow”.
Of course nobody has ever hurled a firecracker at nearly the speed of light over a distance several times farther than the moon. So how do we know that time really obeys the metric equation?
One of the most direct actual experiments to test the metric equation uses elementary particles called muons, which have their own built-in “fuses”. We know from studying muons at rest that they spontaneously decay (into an electron and a pair of neutrinos) with a half-life of about 1.5 microseconds ($\mu\textrm{s}$). This means that the time when any particular muon will decay is random, such that it has a 50% chance of decaying during any 1.5 $\mu\textrm{s}$ time interval.
Conveniently, muons are constantly being created in earth’s upper atmosphere by the collisions of cosmic rays (mostly protons) with air molecules. The muons (unlike the cosmic ray protons) penetrate our atmosphere quite readily, and are constantly raining down on earth’s surface at a rate of about one per square centimeter per minute. We can then detect them with Geiger counters or other detectors used in nuclear physics laboratories.
In one version of the muon experiment, scientists from MIT operated their muon detector in two different locations: on the MIT campus (at approximately sea level), and on the summit of New Hampshire’s Mt. Washington, 6000 feet (or 6 light-microseconds) above sea level. They designed their apparatus to detect muons only within a narrow range of speeds, then counted how many muons with speeds in that range arrived per unit time at each elevation, in order to test whether the muons’ internal “clocks” obey the metric equation.
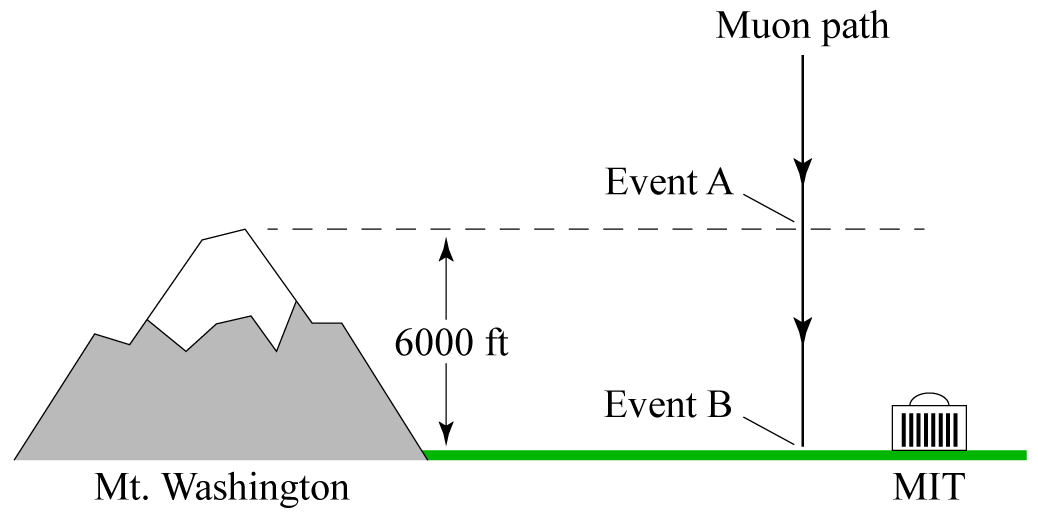
Consider, for instance, a muon that happens to be moving directly downward toward the MIT campus. Let Event A be its crossing the 6000-foot altitude level, and let Event B be its arrival in the detector. If the muon is moving at nearly the speed of light, then the coordinate time interval between these events, as measured in earth’s frame of reference, is $\Delta t_{AB} \approx 6~\mu\textrm{s}$. That’s four times the muons’ half-life, so if we didn’t know anything about relativity we would predict that once the muon makes it to the 6000-foot level, it has only a 1-in-16 chance ($\frac12\cdot\frac12\cdot\frac12\cdot\frac12$) of making it down to sea level without decaying first. On average, therefore, we would expect to detect only 1/16 as many fast-moving muons at MIT as on the top of Mt. Washington.
But according to the metric equation, the muon’s internal clock does not measure 6 seconds of time between Event A and Event B. Because the muon is present at both events (and doesn’t accelerate significantly in between), it measures the spacetime interval,
\begin{equation} \Delta s_{AB} = \Delta t_{AB}\sqrt{1-(v/c)^2} = (6~\mu\textrm{s})\sqrt{1-(v/c)^2}, \end{equation}where $v$ is the muon’s speed with respect to the earth. If, for instance, $v/c = 0.995$, then $\sqrt{1-(v/c)^2}=0.1$, and the time measured by the muon’s clock is only 0.6 microseconds, less than a single half-life. Relativity therefore predicts that the number of muons with this speed detected at MIT should be not 1/16 as many as on Mt. Washington, but well over half as many.
And that’s what the experiment found: The number of muons observed at MIT, compared to Mt. Washington, was much larger than the naive prediction without time dilation, and fully consistent with the prediction of the metric equation.
The MIT experiment is documented in this 1963 film, which is worth watching just to see the old apparatus and counting techniques. It’s also written up in the American Journal of Physics 31, 342-355 (unfortunately paywalled). If you watch the film or read the paper you’ll see that the experiment involved a number of complications that I’ve glossed over. Most importantly, the muons decelerate slightly as they descend through the atmosphere, so the researchers had to account for some deceleration in their quantitative check of the metric equation. But even without sophisticated calculations, the data plainly show that the number of muons arriving at sea level is far too high to account for without relativistic time dilation.
I also recommend this Minute Physics description of the muon experiment.
Another type of unstable subatomic particle is the charged pion, whose half-life is just 18 nanoseconds. Imagine a beam of charged pions traveling down the length of a long vacuum pipe at an accelerator laboratory at speed $0.98c$. (a) If time were absolute, so the spacetime interval were the same as coordinate time, how far would these particles travel before half of them decay? (b) How far do they actually travel before half of them decay, taking the metric equation into account?
Muons weren’t discovered until 1936, so you may still be wondering how Einstein figured out the metric equation in 1905. One line of reasoning that he described involves another thought experiment.
Imagine two horizontal mirrors, facing each other, separated by some fixed vertical distance $d$. Between the mirrors we set off a strobe that emits a single brief pulse of light moving vertically. This light pulse then repeatedly bounces up and down between the mirrors. To measure the time it takes to bounce up and down, we affix a clock to the bottom mirror.
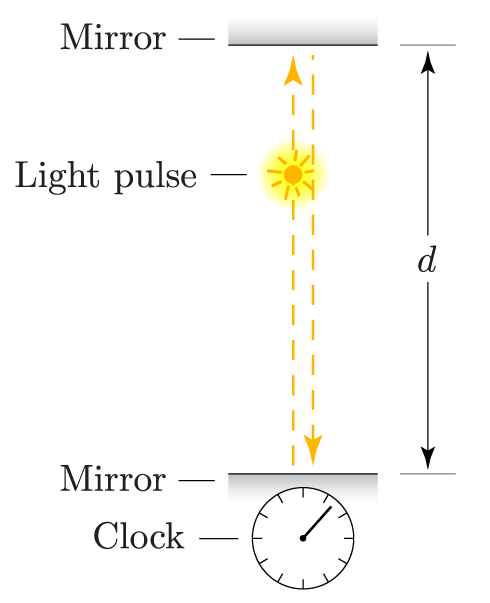
Let Event A be a particular bounce of the light pulse off the bottom mirror, and let Event B be the next bounce off the bottom mirror, after a single round trip. Because the light travels a total distance $2d$ in between these events, and it moves at speed $c$, we can immediately write
\begin{equation} 2d = c\,\Delta s_{AB}, \end{equation}where $\Delta s_{AB}$ is the time between the two events as measured by our clock. Our clock measures the spacetime interval because it is present at both events (and we won’t allow the apparatus to accelerate).
Now let’s view these same events from an inertial reference frame in which the whole apparatus is moving to the right at some constant speed. The illustration below shows three successive images of the mirrors from this perspective (at the times of the three light pulse bounces), along with the path of the light pulse. Notice that in this frame of reference the light pulse is traveling diagonally, so it travels farther. But the principle of relativity (together with the laws of electromagnetism) requires that the measured speed of light still has the same value, $c$, in this new frame of reference. Because the light travels a greater distance at the same speed, it must take more time.
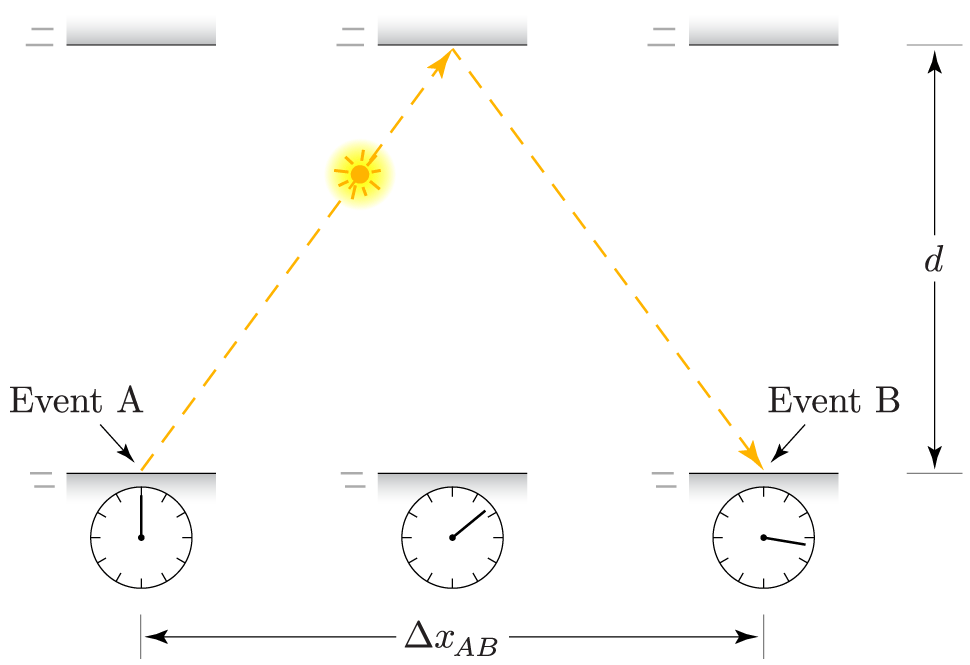
To measure the time between Event A and Event B in our new frame of reference, we require a pair of previously synchronized clocks, at rest in this frame, one present at each event. (These two clocks are not shown in the illustration, which shows only the clock attached to the bottom mirror.) The distance between these two clocks is $\Delta x_{AB}$, so each of the two diagonal legs of the light-pulse path is the hypotenuse of a right triangle with height $d$ and base $\Delta x_{AB}/2$. We can therefore write the total distance traveled by the light pulse, using the Pythagorean theorem, as
\begin{equation} \text{Total distance} = 2\sqrt{d^2+(\Delta x_{AB}/2)^2} = \sqrt{(2d)^2+(\Delta x_{AB})^2}. \end{equation}But since the pulse travels at speed $c$, this distance must equal $c\,\Delta t_{AB}$. Meanwhile we have already seen that $2d = c\,\Delta s_{AB}$, so this equation becomes
\begin{equation} c\,\Delta t_{AB} = \sqrt{(c\,\Delta s_{AB})^2+(\Delta x_{AB})^2}, \end{equation}and this is just an algebraic rearrangement of the metric equation as written above (with the factor of $c$ explicit so we can express $\Delta x_{AB}$ in traditional distance units if we like).
In this lesson I’ll work out two further implications of the metric equation. The first involves proper time measured by a clock that accelerates. The second involves the relativity of distance measurements.
Alice and Betty are identical twins, but their abilities and ambitions are not quite identical. Alice grows up to become an astronomer, while Betty trains to become an astronaut. Their interests align, however, when Alice discovers evidence that one of the planets near Alpha Centauri, the nearest star system to our own, has conditions suitable for life. Betty is chosen to fly on a spaceship and visit the Alpha Centauri system, to investigate further.
The spaceship is launched on the twins’ 30th birthday, and soon Betty is flying toward Alpha Centauri (which is 4 light-years away from earth) at a speed of 4/5 the speed of light. When she finally arrives at the planet of interest, however, she discovers that although it has conditions suitable for life, no life actually exists on its barren surface. Having nothing further to do there, Betty immediately gets back on her spaceship and returns to earth, again at 4/5 the speed of light.
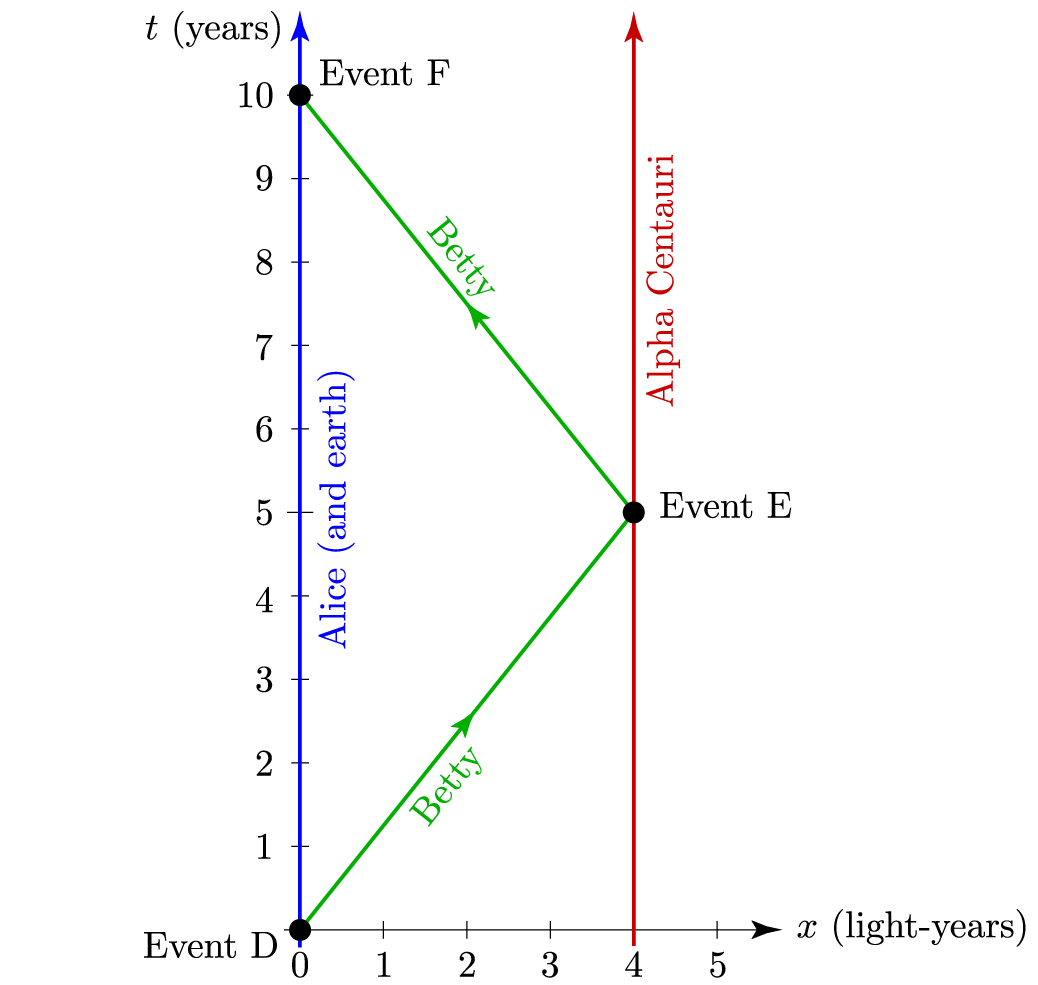
Although the mission’s outcome is a disappointment, both twins are eager to be reunited. But when does their reunion occur? From Alice’s viewpoint, Betty’s spaceship must travel 4 light-years outward at 4/5 the speed of light, so it takes 5 years to reach Alpha Centauri, and another 5 years to return. Ten years pass in total, so Alice will be 40 years old upon Betty’s return. We can easily visualize these events on a spacetime diagram:
But how much time passes from Betty’s perspective?
To answer this question we need to break up Betty’s trip into two segments, connecting three events. As shown on the diagram, Event D is Betty’s departure from earth; Event E is her exploration and turning around at Alpha Centauri; and Event F is her final return to earth. During her outbound journey, Betty’s clocks (including her biological “clock”) measure the spacetime interval $\Delta s_{DE}$, because she is present at both Event D and Event E, and she travels at constant velocity. (I’m assuming, quite unrealistically, that her acceleration and deceleration happen too quickly to show on the diagram or to affect the calculations.) And according to the metric equation, this time interval is
\begin{equation} \Delta s_{DE} = \sqrt{(\Delta t_{DE})^2-(\Delta x_{DE})^2} = \sqrt{(5~\textrm{years})^2 - (4~\textrm{years})^2}=3~\textrm{years}. \end{equation}Similarly, during the return journey, Betty’s clocks measure the spacetime interval $\Delta s_{EF}$, which also equals 3 years. The total time elapsed during the journey, according to Betty’s clocks, is therefore only 6 years! When they are reunited and Alice is turning 40, Betty is only turning 36.
This result is astounding, but there’s just no getting around it if you accept the metric equation. What some people have trouble understanding, though, is how to reconcile the asymmetry in the twins’ ages with the principle of relativity. If motion is relative, shouldn’t it be equally valid to analyze these same events from the viewpoint of Betty’s reference frame? And in Betty’s frame, wouldn’t it be Alice who races away (along with the earth) at 4/5 the speed of light, then turns around and returns at the same speed, and who therefore ends up being the younger twin when they are reunited at Event F?
No. The two sisters’ reference frames are not equally valid because Alice’s frame is inertial (to a good approximation) and Betty’s is not. It is Betty, not Alice, who experiences enormous accelerations (“g-forces”) as her spaceship speeds up during launch, turns around at Alpha Centauri, and finally comes to a screeching halt when she returns to earth. The principle of relativity says not that all reference frames are equally valid, but that all inertial reference frames are equally valid. The concepts and tools we’ve developed in these lessons tell us nothing about how to analyze events from the perspective of a non-inertial reference frame.
But we don’t need any new tools to analyze the motion of accelerated objects, such as Betty and her spaceship, as viewed from any inertial frame of reference. More specifically, this example shows us how to calculate the proper time between two events as measured by an accelerated clock: just break up the clock’s worldline into segments along which the velocity is (approximately) constant, apply the metric equation to each of these smaller segments, and add up the $\Delta s$ values for each segment to get the proper time, $\Delta\tau$, measured by the accelerated clock. In Betty’s case it suffices to break the worldline DEF into just two segments, DE and EF, but in other cases we might need more than two, and for a smoothly accelerated clock we would need to divide the curved worldline into a large number of small, nearly straight segments.
Moreover, it isn’t hard to prove that for any given pair of events, the proper time interval $\Delta \tau$ measured by any accelerated clock (present at both events) will always be less than the spacetime interval $\Delta s$, that is, the time measured by a non-accelerated clock (present at both events). Betty’s younger age compared to Alice is just a special case of this general fact about spacetime.
Of course nobody (at least here on earth) has access to spaceships that actually travel at 4/5 the speed of light. You may therefore be wondering what real-world experiments have been done to verify that an accelerated clock measures less time, between the same two events, than a non-accelerated clock. These experiments fall into two categories. First, you can again use sub-atomic particles such as muons, traveling at high speeds. In one experiment in the 1970s, scientists at the CERN laboratory in Geneva measured the decay of muons while they were accelerating around a storage ring at $v/c\approx 0.9994$, and found that on average these muons lasted 29 times longer (or “aged” 29 times slower) than non-accelerated muons, just as relativity predicts. Second, you can avoid the need for absurdly high speeds if you use sufficiently accurate clocks. In a famous experiment performed in 1971, scientists flew state-of-the-art cesium beam atomic clocks around the world on commercial aircraft, comparing the clock readings to those of an identical clock that remained at the U.S. Naval Observatory. Again, the results were fully consistent with the predictions of relativity.
Cedric and Denzel are twins, and both wish to travel from earth to the Sirius star system, 9 light-years away. Cedric departs on their 25th birthday, taking a spaceship that travels at 3/4 the speed of light. Denzel procrastinates and doesn’t depart until two years later, but is then able to take a newly developed spaceship that travels at 9/10 the speed of light. (a) Draw an accurate spacetime diagram showing the worldlines of earth, Sirius, and both of the twins. Label each of the departure and arrival events. (b) How old is each of the twins when they simultaneously arrive at Sirius? Explain how your answers illustrate that the proper time between two given events along an accelerated worldline is always less than the spacetime interval.
A muon travels around a circular storage ring at constant speed $v$. Let Event A be its passing by some fixed point in the ring, and let Event B be its next passing by that same point, after one trip around the ring. Prove that the time between these events as measured by the muon’s clock is $\Delta\tau_{AB}=\sqrt{1-(v/c)^2}\Delta s_{AB}$, where as usual $\Delta s_{AB}$ is the time between these two events as measured by a non-accelerated clock. (Hint: Imagine dividing the muon’s circular trip into many small segments that are each essentially straight.)
Now let’s return to the cosmic-ray muon experiment described in the previous lesson. The principle of relativity tells us that it is equally valid to analyze this experiment from the reference frame of one of the muons, in which it is at rest and the earth’s surface is rushing upward toward it at, say, 99.5% of the speed of light. But as I calculated above, the time interval between Event A (summit of Mt. Washington rushes past muon) and Event B (ground at sea level smashes into muon) is only 0.6 microseconds in this frame of reference. How is that possible, if Mt. Washington’s height is 6 light-microseconds?
The answer is that in this frame of reference, the mountain is not 6 light-microseconds high. Instead it is only 0.6 light-microseconds high (about 600 feet), because whenever we observe an object from a reference frame in which it is moving at speed $v$, it appears shorter, along the direction of motion, by a factor of $\sqrt{1-(v/c)^2}$. In the muon’s reference frame, the situation looks something like this:
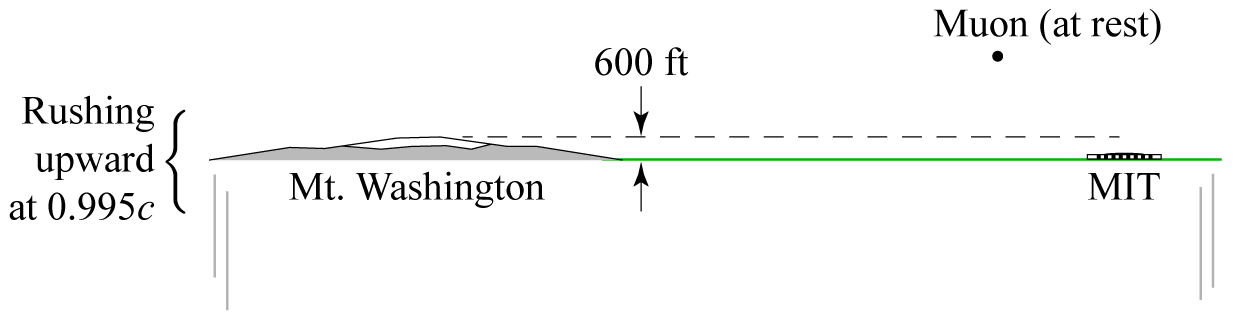
With the mountain’s height contracted by a factor of 10, it passes the stationary muon in 0.6 microseconds.
More generally, if we denote an object’s true length (in the frame in which it is at rest) as $L_0$ and its measured length (in the frame in which it’s moving, along the direction of this length, at speed $v$) as $L$, then the general formula for this relativistic length contraction effect is
\begin{equation} L = L_0\sqrt{1-(v/c)^2}. \end{equation}So $L$ for a moving object is always less than $L_0$, and the difference between $L$ and $L_0$ is negligible when $v\ll c$.
By now you’ve surely noticed that the expression $\sqrt{1-(v/c)^2}$ comes up a lot in relativity. For convenience we therefore often use a standard abbreviation for it, or actually for its reciprocal:
\begin{equation} \gamma = \frac1{\sqrt{1-(v/c)^2}}. \end{equation}The symbol is the Greek letter gamma, and this quantity is often called the Lorentz factor, after the Dutch physicist H. A. Lorentz, who derived many of the formulas of relativity several years before Einstein (but arguably didn’t fully understand their meaning, as Einstein did). The Lorentz factor equals 1 when $v=0$, and increases to infinity as $v$ approaches the speed of light. In terms of the Lorentz factor, the metric equation reads $\Delta t_{AB} = \Delta s_{AB}\cdot \gamma$ and the length contraction formula reads $L=L_0/\gamma$. The main downside of using this abbreviation is that in some situations there can be more than one relevant velocity, and then you need to be clear about which velocity your $\gamma$ abbreviation depends on.
A 50-foot (50 light-nanosecond) log is lying on the ground. A bird flies past the log, just above it and parallel to its length, at 3/5 the speed of light. Let Event A be the bird passing the first end of the log, and let Event B be the bird passing the other end of the log. (a) Draw an accurate spacetime diagram, from the viewpoint of earth’s reference frame, showing the worldlines of both ends of the log, the worldline of the bird, and Events A and B. (b) What is the time between Events A and B, as measured by the squirrels sitting on the log? (c) What is the time between Events A and B, as measured by the bird? (d) From the bird’s point of view, the log is rushing past at 3/5 the speed of light. How far does the log move, during the time between Events A and B, according to the bird’s calculations? Explain carefully.
While peacefully watching cloud formations in the desert, you suddenly see a roadrunner zip by (beep, beep!) at half the speed of light, pursued by a coyote running at the same speed. According to your measurements, the coyote is ten meters behind the roadrunner. How far behind does the roadrunner think the coyote is? (Hint: If the two creatures were holding a pole between them, in whose reference frame would the pole be moving?)
By how much is the length of a 100-meter-long commuter train contracted in a reference frame in which it is moving at 30 m/s? (Hint: You may find it helpful to use the binomial approximation, $(1+\epsilon)^n\approx 1+n\epsilon$, which is accurate when $|n\epsilon|$ is much less than 1.)
Let’s do another thought experiment. I’m standing at position zero in my carefully constructed inertial reference frame, armed with a strobe lamp. Some distance away in the $+x$ direction I’ve placed a mirror, anchored to my frame, facing me. At a certain time I flash my strobe lamp (Event F), sending a single light pulse outward toward the mirror. The pulse bounces off the mirror (Event B) and returns toward me so that I see it (Event S) some time later.
Here is a spacetime diagram showing these events:
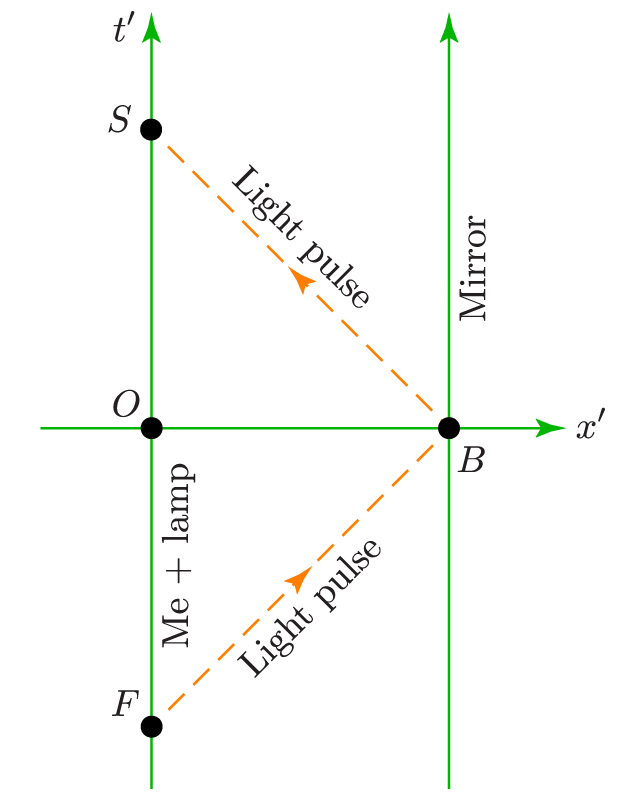
I’ve placed the origin event (Event O, when my wristwatch reads zero) half-way between Events F and S. This arbitrary choice of when the time is zero isn’t terribly important, but it creates a nice symmetry in the diagram. The important feature is that whatever event is half-way between F and S must occur at the same time as Event B. I know this because light always travels at the same speed, and the light had to travel the same distance on its outward and return trips, so those half-trips must have required equal amounts of time. I’ve drawn the light signal worldlines at 45-degree angles, because light always travels at exactly one light-second per second.
Perhaps you can guess what we’re going to do next: view all these events from a different reference frame (“yours”), in which my entire laboratory (including me, my strobe lamp, and the mirror) is moving—let’s say at half the speed of light in the $+x$ direction. And we’ll draw a second spacetime diagram of the very same events, from your point of view.
On your spacetime diagram, my worldline runs diagonally up and to the right, with a slope of 2 (seconds per light-second), since my velocity (in light-seconds per second) is 1/2. Let’s label your time and space axes as $t$ and $x$, and (to distinguish them) label my axes as $t'$ and $x'$, as I’ve already done on the diagram above. Notice that the $t'$ axis is the same as my worldline, with a slope of 2 on your spacetime diagram. This axis is the line connecting all events that happen at the spatial origin ($x'=0$) in my reference frame, just as the $t$ axis connects all events happening at the spatial origin ($x=0$) in your reference frame. Because I’m moving with respect to you, our time axes are different—and I hope you agree that there’s nothing surprising about this fact.
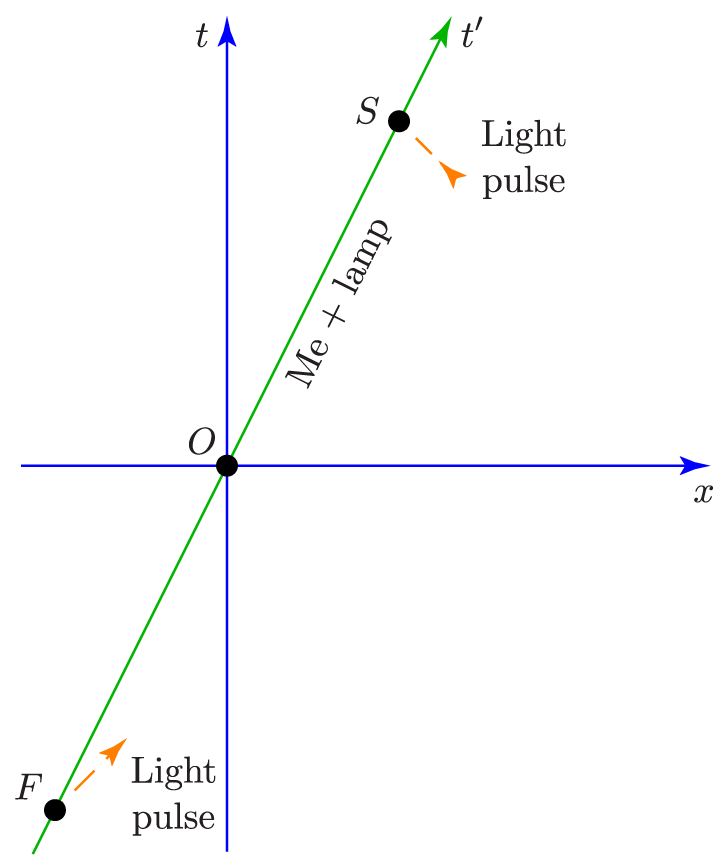
For simplicity I’ve drawn this diagram so that the origin events of our two reference frames coincide. I’ve drawn Events F and S at appropriate points on my worldline, so that the origin event O is again half-way between them.
Question: Where on this diagram should I locate Event B?
To answer this question we use the startling fact that you also measure the light pulse to move at exactly one light-second per second, despite the fact that the strobe lamp that emitted the pulse is moving (with respect to you) at half that speed. That seems impossible, right? But please suspend your disbelief for a while, so we can work out the logical consequences. If you really measure the light to be traveling at one light-second per second, then we must draw the light-pulse worldlines at 45-degree angles even on your spacetime diagram. I started them on the diagram above. Extrapolating each of them to the right, we can locate Event B at the unique point where these 45-degree lines intersect:
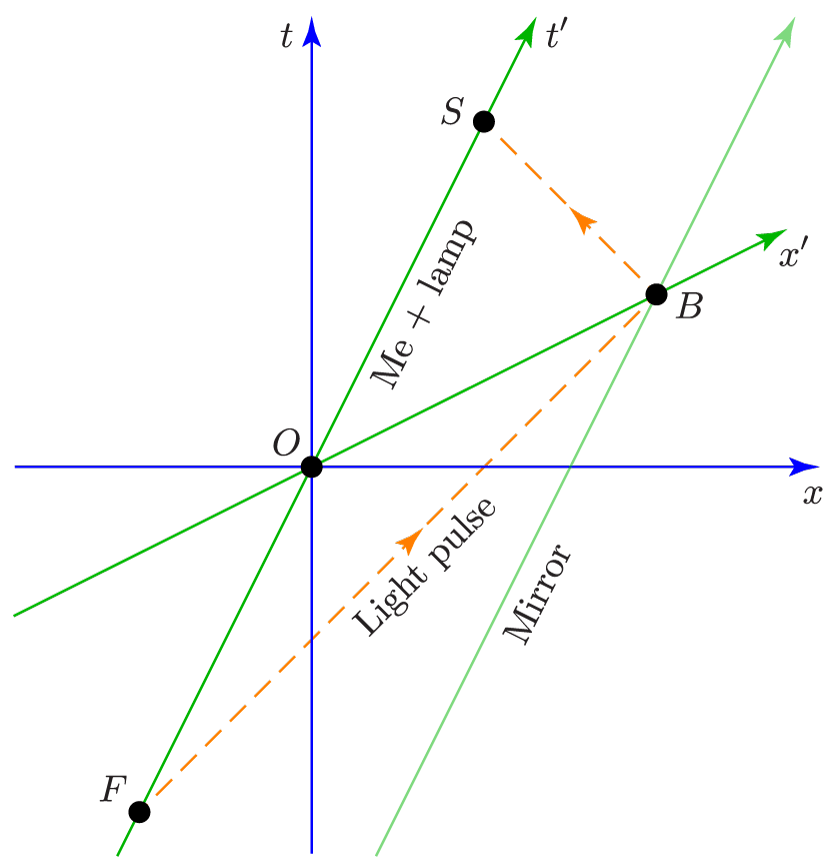
And what we find is that even though Events O and B are simultaneous in my reference frame, they are not simultaneous in yours: You observe Event B to occur after Event O, at some positive $t$ value. More generally, when two events occurring in different places are observed to be simultaneous from one frame of reference, they will be observed to occur at different times from a frame of reference that is moving, with respect to the first, along the direction that separates the events. This phenomenon is called relativity of simultaneity.
To emphasize the relativity of simultaneity, I’ve added another element to the diagram: the $x'$ axis. What do I mean by the $x'$ axis? It’s the line connecting all events that happen at time zero in my reference frame, that is, at $t'=0$. (Compare the $x$ axis, which connects all events that happen at $t=0$, and the $t$ and $t'$ axes, which are lines connecting all events that happen at $x=0$ and $x'=0$, respectively.) In our case, the $x'$ axis must connect events O and B, because they both occur at $t'=0$.
Notice that the $x'$ axis is sloped upward from the $x$ axis by the same amount that the $t'$ axis is sloped rightward from the $t$ axis. Or, equivalently, the angle between the $x$ and $x'$ axes is the same as the angle between the $t$ and $t'$ axes. In the present case, where my frame is moving with respect to yours in the $+x$ direction at $v/c=1/2$, the $t'$ axis has slope 2 while the $x'$ axis has slope 1/2. (I won’t present a rigorous proof that the slopes are always related in this way, but the proof isn’t hard. If you’d like to try it, draw another light-signal worldline passing through Event O and then look for similar triangles.)
A spacetime diagram showing two sets of axes, for two different reference frames, is called a two-observer spacetime diagram. To use the diagram quantitatively, we can add gridlines for both coordinate systems:
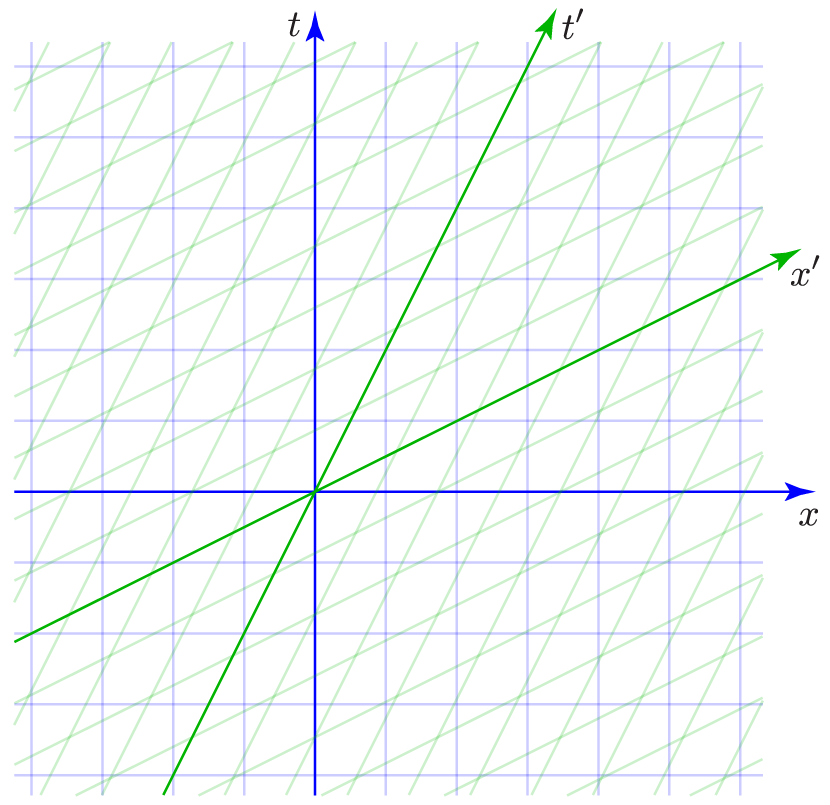
For the unprimed frame (“yours”, shown in blue), each vertical gridline connects all the events happening at a particular place (as measured in your frame), while each horizontal gridline connects all the events happening at a particular time (as measured in your frame). We can use whatever unit we like for the interval between gridlines, with the understanding that the space interval is however far light travels in one time interval.
For the primed frame (“mine”, shown in green), each mostly-vertical gridline connects all the events happening at a particular place (as measured in my frame), while each mostly-horizontal gridline connects all the events happening at a particular time (as measured in my frame). Importantly, I’ve spaced these gridlines so they correspond to the same time and space intervals as the gridlines in your frame. How did I do this? Using the metric equation! For instance, if Event P lies on the $t'$ axis where the $t'=1$ gridline crosses this axis, then my wristwatch measures a spacetime interval $\Delta s_{OP}=1$. But according to the metric equation, your clocks should measure Event P to occur at $\Delta t_{OP} = \gamma\cdot \Delta s_{OP} = 1/\sqrt{1-(1/2)^2} = 1.155$, as shown in this enlarged portion of the diagram:
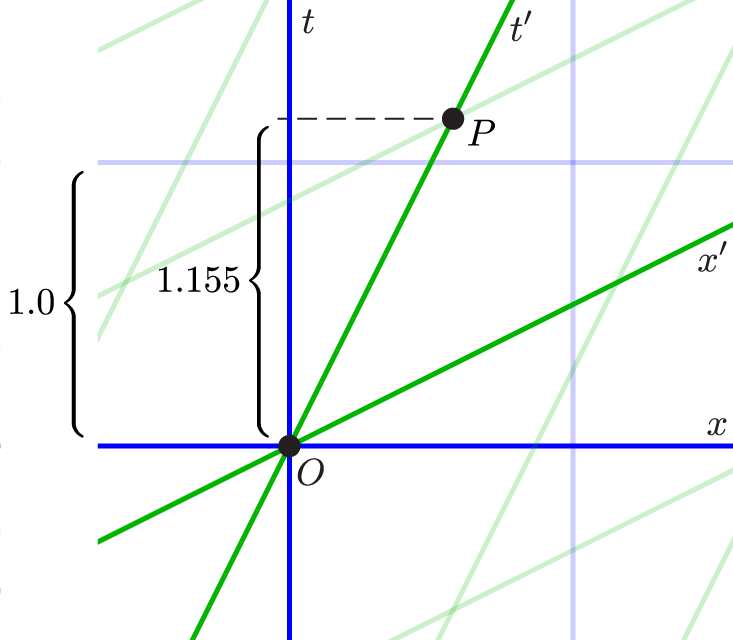
This particular two-observer spacetime diagram is drawn for a primed frame moving with respect to the unprimed frame in the $+x$ direction at a speed of 1/2 the speed of light (half a unit of distance in each unit of time). You can download a printable page of “relativistic graph paper”, also drawn for $v/c=1/2$, at this link. To see what the gridlines would look like for other choices of the relative velocity of the two reference frames, check out this cool web app by Prof. Steven Sahyun of the University of Wisconsin at Whitewater.
Once we have our relativistic graph paper, we can plot events on it according to one reference frame, then read off their coordinates in the other reference frame:
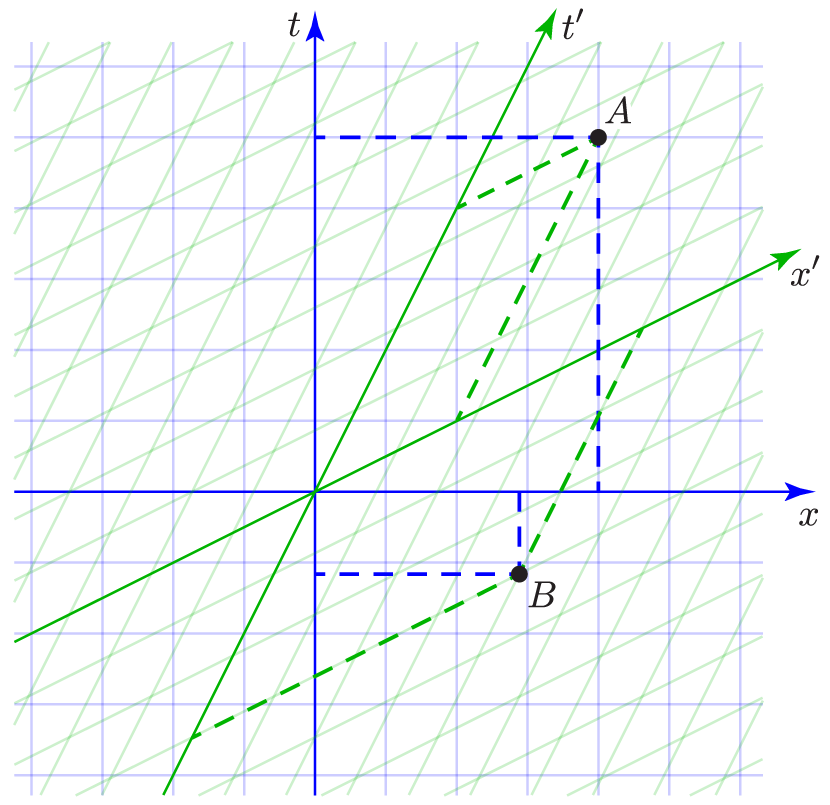
Here I’ve plotted Event A at $t=5$ and $x=4$, as indicated by the blue dashed lines. Then, using the green dashed lines, we can read off the approximate primed-frame coordinates $t'\approx3.5$ and $x'\approx1.7$. Similarly, I plotted Event B at $t'=-3$ and $x'=4$, as indicated by the second pair of dashed green lines. But as the second pair of dashed blue lines shows, the approximate coordinates of this same event in the unprimed frame are $t\approx-1.15$ and $x\approx2.9$.
These coordinate transformations have the crucial property that if you square the time and space coordinates and then subtract, you get the same thing in either reference frame:
\begin{equation} (t')^2 - (x')^2 = t^2 - x^2. \end{equation}For instance, for Event A, the right-hand side is $5^2 - 4^2 = 9$, while the left-hand side is approximately $(3.5)^2-(1.7)^2\approx9$. But computed in either frame, this quantity is just the square of the spacetime interval between the origin event (call it O) and Event A, that is, $(\Delta s_{OA})^2$. Because the spacetime interval between two events is the unique time between those events as measured by a single non-accelerating clock that’s present at both events, we must obtain the same spacetime interval when we compute it using the coordinates in either reference frame. This “invariance” of the spacetime interval is analogous to how you can calculate the squared distance between two points in ordinary two-dimensional space as $(\Delta x)^2+(\Delta y)^2$, and you’ll get the same result no matter how you orient your $x$ and $y$ axes. (Note, however, that the “Pythagorean theorem” for spacetime intervals has a minus sign where the ordinary Pythagorean theorem for two-dimensional space has a plus.)
As you might guess, there are also equations that you can use to carry out these kinds of transformations between primed and unprimed spacetime coordinates. They’re called the Lorentz transformation equations, and you can find them in just about any textbook on relativity. They’re analogous to the trigonometric equations that transform coordinates in ordinary two-dimensional space when we rotate the axes $(x,y)$ by some angle. (The Lorentz transformation equations can be written in terms of the hyperbolic sine and cosine of the “angle” whose hyperbolic tangent is $v/c$.)
Event C occurs at $t=1$ and $x=-2$ in the unprimed reference frame. What are its coordinates in the primed reference frame represented in the diagrams above, moving rightward at half the speed of light with respect to the unprimed frame? Show your construction on a copy of the two-observer spacetime diagram. Also check that $(t')^2 - (x')^2 = t^2 - x^2$.
Event D occurs at $t'=1$ and $x'=4$ in the primed reference frame represented in the diagrams above. What are its coordinates in the unprimed frame, which is moving leftward at half the speed of light with respect to the primed frame? Show your construction on a copy of the two-observer spacetime diagram. Also check that $(t')^2 - (x')^2 = t^2 - x^2$.
At high noon, a solar flare erupts on the surface of the sun. Half an hour later, at 12:30, a comet crashes into Jupiter, 780 million km away from the sun. (These data are as measured in earth’s reference frame, which is moving at negligible speed with respect to the sun and Jupiter.) Meanwhile an alien spaceship zips by at $0.8c$, headed in the direction from the sun toward Jupiter. (a) Draw a spacetime diagram, calibrated in minutes of time and light-minutes of space, showing the sun, Jupiter, the flare eruption, and the comet crash. (b) Add $t'$ and $x'$ axes for the alien spaceship’s reference frame, and determine which event (solar flare or comet crash) occurs first in the aliens’ frame. (c) Which of the two events do the aliens see first? Draw worldlines to represent the light from each event traveling toward the alien spaceship, and show that the answer depends on where the spaceship is located within its reference frame (which I haven’t specified).
Redraw the two-observer spacetime diagram in the text above from the viewpoint of the primed reference frame, so the $t'$ axis points straight up and the $x'$ axis points straight to the right. Since the unprimed frame is now moving to the left at half the speed of light, this means that the $t$ axis will point up and to the left, with a slope of $-2$. Plot Event A according to its unprimed coordinates, and check that its primed coordinates are the same as what I found above. Plot Event B according to its primed coordinates, and check that its unprimed coordinates are the same as what I found above.
Draw a calibrated two-observer spacetime diagram for the case where the primed frame moves at $v=0.7c$ with respect to the unprimed frame. What are the primed coordinates of an event that occurs at $t=5$ and $x=6$? What are the unprimed coordinates of an event that occurs at $t'=-2$ and $x'=4$?
Draw a two-observer spacetime diagram for an imaginary universe in which time is absolute, so $t'=t$ for every event. Label the axes and include gridlines.
One handy use of a two-observer spacetime diagram is to give us a better perspective on length contraction. Suppose there’s a four-unit-long stick that’s at rest with respect to the primed frame, with one end at $x'=0$ and the other end at $x'=4$:
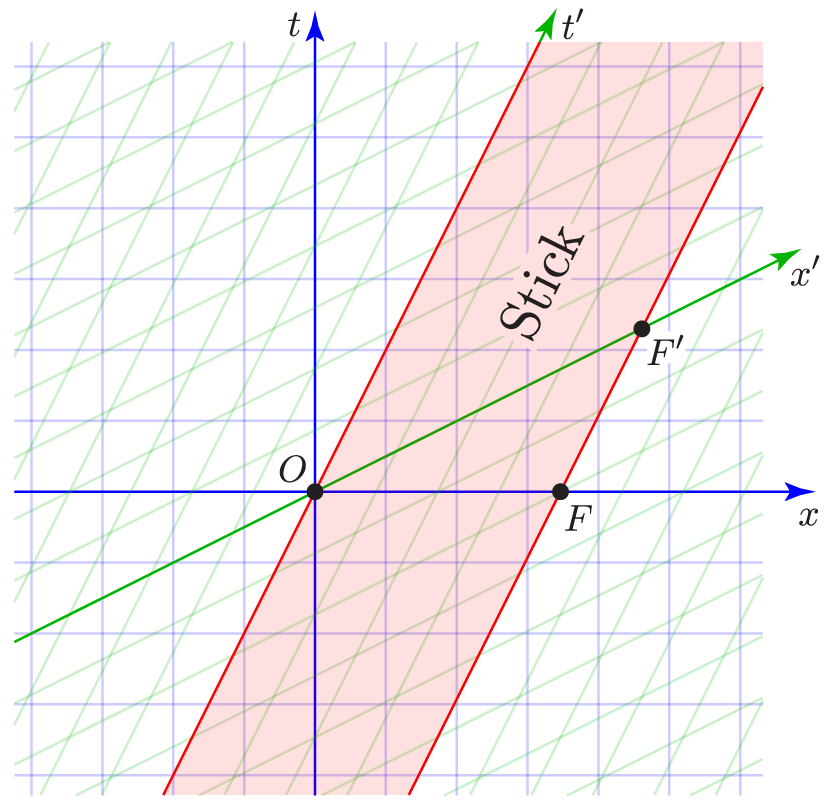
I’ve drawn the worldlines of each end of the stick in red, and shaded the spacetime region in between to highlight what we might call the stick’s world-sheet. You can plainly see that the stick is four units long as measured in the primed frame, because events O and F${}'$, which are simultaneous in the primed frame, are four grid-spacings apart along the $x'$ axis. But how long is the stick in the unprimed frame? To answer that question we should find two events, one at each end of the stick, that are simultaneous in the unprimed frame. The most convenient such events are O and F, and as you can also plainly see, they are only about 3.5 units apart along the $x$ axis. The stick appears length-contracted from the unprimed frame, in which it is moving.
To check for consistency, let’s look next at what happens if the stick is at rest with respect to the unprimed frame:
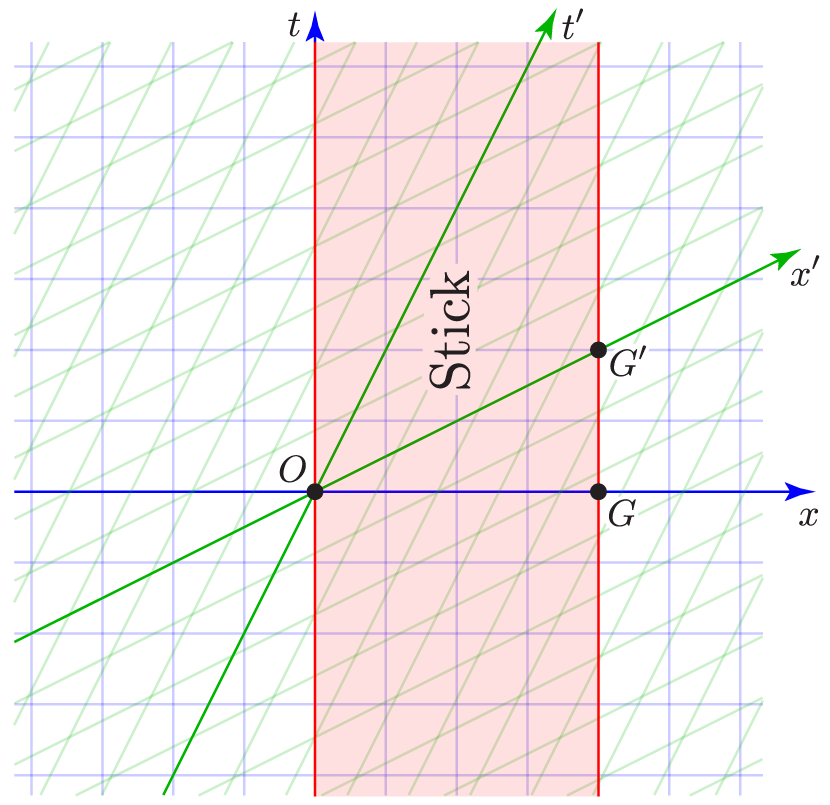
Now to determine the length in the unprimed frame we can look at events O and G, which are four units apart along the $x$ axis. But to determine the length in the primed frame we should look (for instance) at events O and G${}'$, which are simultaneous in the primed frame. And sure enough, these events are only about 3.5 grid spacings apart, as measured along the $x'$ axis.
Length contraction is really best understood as a side-effect of the relativity of simultaneity: Different observers disagree on which pairs of events (one at each end of the stick) are simultaneous, and therefore they disagree about how far apart these events are, which is what they mean by the stick’s length. An analogous phenomenon in ordinary two-dimensional space would be how the width of a road appears different, depending on whether you cross it at a right angle or at some other angle. But whereas the road appears wider when you cross it along a diagonal, the minus sign in the metric equation makes a stick appear shorter when you view it from a reference frame in which it is moving.
Use the length contraction formula to check that a stick with a rest length of 4 units should appear roughly 3.5 units long in a reference frame in which it is moving at half the speed of light.
You own a 10-foot ladder that you would like to store inside an 8-foot-long shed. Having studied relativity, you figure you can do it as long as you run fast enough, holding the ladder horizontally so its contracted length is just 8 feet. (How fast is that?) But before putting your plan into action, you explain it to your spouse, who expresses skepticism: “In your frame of reference, won’t the ladder still be 10 feet long, while the moving shed is contracted to 80% of its usual length, that is, just 6.4 feet? A 10-foot ladder won’t fit inside a 6.4-foot shed!” Now you’re both puzzled. How can the ladder fit (even momentarily) inside the shed as viewed from one reference frame, but not fit as viewed from another frame? Does this paradox prove that relativity is illogical nonsense? To resolve the paradox, draw a two-observer spacetime diagram showing the shed (at rest) and the ladder (in motion), identifying the key events when/where the ends of the ladder pass the ends of the shed. For the sake of safety, please assume that the shed has an open door at each end. Explain carefully what happens from the perspective of each frame of reference, and why there is no logical contradiction.
Now let’s move on to a completely new example. Suppose I’m at rest in the primed frame, moving with respect to you in the positive direction at half the speed of light, and I toss a baseball forward at half the speed of light with respect to me. How fast is the baseball moving with respect to you?
If you didn’t know anything about relativity, you would probably answer this question by adding one-half to one-half to obtain one, that is, one times the speed of light. But by now you may be more wary of such simple answers.
To answer this question I’ve carefully drawn the baseball’s worldline on a two-observer spacetime diagram below. I started the worldline at the origin and then, looking only at the diagonal green gridlines, measured one unit of space (along the $x'$ axis) and two units of time (parallel to the $t'$ axis), to find another event along the worldline, under the assumption that I measure the baseball to be moving at half the speed of light. I then repeated this process to extend the worldline further, and also extended it backward from the origin. The events that I used to draw this line are highlighted with red dots, and you’ll notice that they’re all at intersections of the green gridlines.
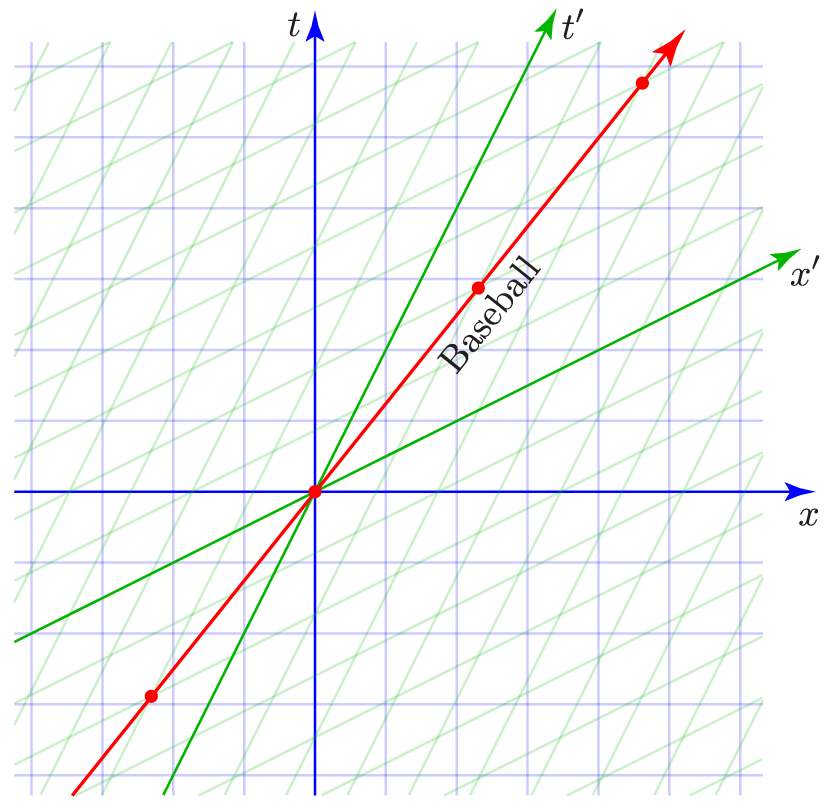
Amazingly, the baseball’s worldline is steeper than 45 degrees, indicating that you measure the ball to be moving somewhat slower than the speed of light. And to find its actual speed, you can just look at the blue gridlines! I’ve conveniently chosen the numbers in this example so the baseball’s worldline passes exactly through the blue grid point at $t=5$ and $x=4$ (check this!), meaning that you measure the ball’s speed to be only 4/5 the speed of light.
This example is a special case of the famous Einstein velocity transformation formula. Before I write the formula in general, I need to carefully define symbols for the three different velocities that we’re talking about:
(Of course the object doesn’t have to be a baseball, but “baseball” seems easier to remember than “object”.) Let’s also agree that all three of these velocities are to be measured as fractions of the speed of light. The general formula is then:
\begin{equation} u_x = \frac{u'_x + v_x}{1+u'_x v_x}. \end{equation}Notice that the numerator of this formula is what we would expect if we didn’t know anything about relativity: just add the two velocities! But the denominator contains a “correction” term that’s the product of the two velocities, measured as fractions of the speed of light. At ordinary speeds these fractions would be tiny and their product would be tinier still, so we could simply neglect this correction term. But when $u'_x=v_x=1/2$, we obtain
\begin{equation} u_x = \frac{\frac12+\frac12}{1+\frac12\cdot\frac12} = \frac1{1+\frac14}=\frac45, \end{equation}just as we already saw from the diagram.
Applying the velocity transformation formula to other examples can be tricky, because it’s not always obvious which reference frame should be the primed frame, which should be the unprimed frame, and which object should correspond to the baseball. There are always multiple correct ways to set up these correspondences, but you need to be consistent. Any of the three velocities is allowed to be negative, and you often need to pay special attention to minus signs. The best advice I can give you is to draw a picture showing which way things are going and which direction you’re calling positive; then write out, in English, exactly what you mean by each of the three symbols. As a check, remember that if you neglect the correction term in the denominator, you should get the answer you would expect if you didn’t know about relativity.
What if, instead of a baseball, I “toss” a light pulse? Assuming that the pulse moves forward at the speed of light with respect to me, while I move at half the speed of light with respect to you, how fast does the light pulse move with respect to you? Answer this question using a two-observer spacetime diagram, then answer it again using the Einstein velocity transformation formula. Finally, do it again (using both methods) for a light pulse that I “toss” in the backward direction.
You are fleeing from Planet Vogsphere at speed $0.99c$ (with respect to the planet) when your spaceship’s antimatter drive malfunctions, making further acceleration impossible. Knowing the Vogons are in hot pursuit, you climb into your escape pod set it to be launched forward at the maximum speed of $0.95c$ (with respect to your spaceship). Once the pod is launched, how fast is it going with respect to Vogsphere?
A supersonic jet, moving with respect to the ground at 1000 m/s, fires a supersonic missile in the forward direction at a speed of 1000 m/s with respect to the jet. What is the missile’s speed with respect to the ground? By what percentage does the answer differ from the naive prediction, 2000 m/s?
A distant quasar is moving away from earth at speed $0.35c$. The quasar emits a jet of plasma in the direction toward earth. Astronomers on earth measure the jet to be approaching at speed $0.27c$. What is the jet’s velocity with respect to the quasar?
As you may now suspect, the rules of relativistic velocity transformations make it impossible to combine two velocities less than 1—or even equal to 1—to obtain a velocity greater than 1. The speed of light (which equals 1 in the units I’m using) seems to be some sort of limit, which you can’t cross by building up to it in stages.
But it’s still fair to ask whether there might be some sort of object or signal that inherently travels faster than the speed of light, much as electromagnetic waves inherently travel at the speed of light. As a final application of two-observer diagrams, let’s ask whether such a thing is possible.
Suppose, for instance, that you have a device capable of sending signals at three times the speed of light. You aim your device at a friend located six light-seconds away in the $+x$ direction, and press the button at $t=0$ (Event O) to send a secret message. Traveling at three times the speed of light, the message should take two seconds to reach your friend; let’s call the arrival of the message Event C. Plotted on a spacetime diagram (from the perspective of your reference frame), the events and the signal’s worldline would look like this:
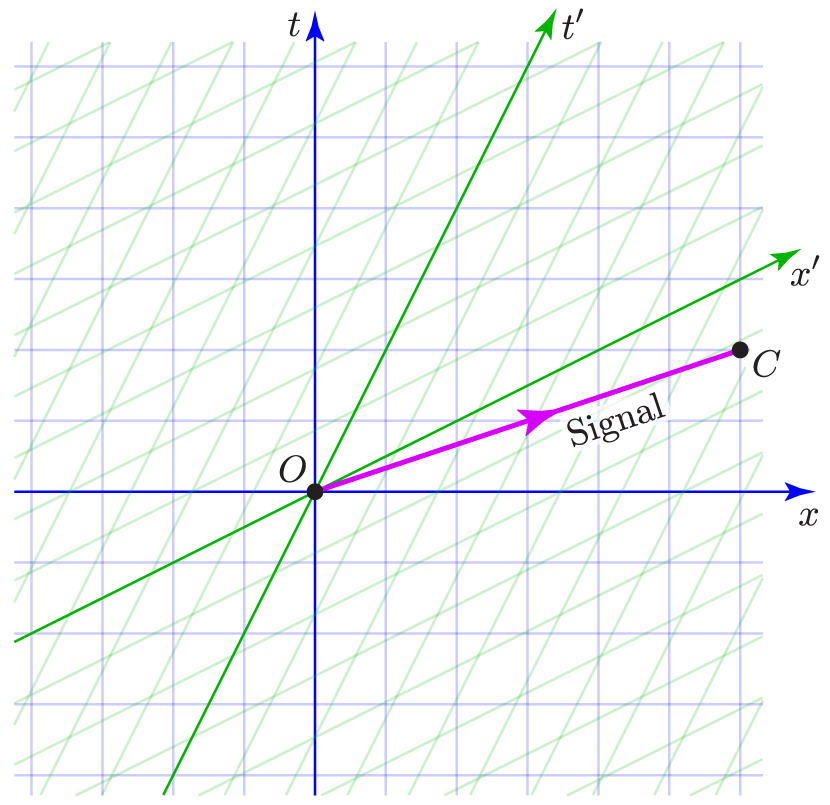
And perhaps you can now see the problem. Although there’s nothing wrong with this diagram from your perspective, it’s nonsense from my perspective, if I’m moving at half the speed of light in the positive direction with respect to you. Whereas you observe a signal traveling from Event O to Event C at three times the speed of light, I observe a signal traveling from Event C to Event O (also at tremendous speed), because in my reference frame Event C occurs before Event O (slightly more than one second before, according to the diagram).
More generally, if you draw any purported worldline representing a signal traveling faster than the speed of light on a spacetime diagram, I can always draw an $x'$ axis for some primed reference frame, moving at less than the speed of light with respect to you, that’s steeper on the diagram than your signal’s worldline. From the perspective of this primed reference frame your signal arrives before it was sent, or equivalently, it goes backwards in time. In short: you show me a signal that travels faster than the speed of light, and I’ll show you a reference frame in which that signal is traveling backwards in time.
Now perhaps the idea of signals going backwards in time doesn’t bother you. But they’re certainly contrary to all of our experience—except, of course, in science fiction stories. Moreover, this idea seems to lead to all sorts of logical paradoxes, such as the question of who really wrote the song “Johnny B. Goode” (in the movie Back to the Future), if Marty McFly learned it from Chuck Berry, but Chuck Berry learned it from a time-traveling Marty McFly.
The easiest way out of this paradox is simply to assume that it’s impossible to send any signals faster than the speed of light. Any signal traveling slower than the speed of light, or even at the speed of light, has a steep enough worldline that it travels forward in time with respect to all inertial reference frames (which we also assume must travel slower than the speed of light). In this context we refer to the speed of light as the cosmic speed limit —a fundamental property of spacetime that affects all measurements and all motion. From this perspective, the fact that electromagnetic waves happen to travel right at the cosmic speed limit is interesting, but the cosmic speed limit itself is more fundamental than electromagnetism.
At exactly 7:00 am, a charge of dynamite explodes at a road construction site in the Rocky Mountains. At 7:00:00.0005 am (half a millisecond later), a mysterious shaking is felt at a diner in Denver (200 km east of the construction site), causing a cup of coffee to fall off the counter. Could the explosion have caused the shaking? To answer this question, draw a spacetime diagram that accurately shows the space and time separations of the two events. Then consider whether there exists a frame of reference in which the shaking occurred before the explosion. If there is such a frame, which way must it be moving with respect to the earth, and how fast? If there is no such frame, how can you tell?
Two-observer spacetime diagrams invite us to think of $t$ and $x$ as two components of a single spacetime vector, analogous to the position vector $(x,y)$ in ordinary two-dimensional space. Just as the components of a position vector change if we use a rotated coordinate system, so also the components of a spacetime vector change if we “boost” to a different inertial reference frame (moving with respect to the original frame). If we include all three dimensions of space, then the coordinates of any event form what we call a four-vector, $(t,x,y,z)$.
In this final lesson I want to tell you about another important four-vector. But before I do, let’s back up and think about why we use vectors in the first place, even in plain old three-dimensional space. The most apparent reason is for brevity of notation: we can write a single equation like
\begin{equation} \vec F = m\vec a \qquad \text{or} \qquad \vec p_\textrm{final} = \vec p_\textrm{initial} \end{equation}instead of writing out three separate equations for the $x$, $y$, and $z$ components. But there’s a more important reason besides brevity. When we write that one vector equals another, we’re making a statement about the vectors themselves, independent of how we orient our coordinate axes to define their $x$, $y$, and $z$ components. This means that if a vector equation is true in one coordinate system, it must also be true in any rotated coordinate system. Writing the laws of physics in terms of vectors doesn’t ensure that these laws are correct, but at least it ensures that they’re consistent with the principle that space doesn’t have any “preferred directions”; our choice of coordinate axes is arbitrary.
In a completely analogous way, writing the laws of physics using four-vectors will ensure that if these laws are true in one inertial frame of reference, then they will be true in all inertial frames of reference. In other words, using four-vectors ensures that the equations we write will be consistent with the principle of relativity.
With this principle in mind, let’s now think about some of the laws of physics.
In Newtonian mechanics, after you learned the kinematic concepts of position, time, velocity, and acceleration, you went on to study dynamics: force, mass, Newton’s second law, and the laws of conservation of momentum and energy.
We could now revisit each of these concepts in the context of relativity, but it turns out that the relativistic version of Newton’s second law isn’t nearly as useful as we might have guessed. Instead it’s more efficient to skip over the concept of force and go straight to the relativistic version of momentum.
Let’s consider a simple one-dimensional momentum conservation problem. A 1-kg block is gliding frictionlessly (or drifting through space) at exactly 20 m/s, toward an identical 1-kg block that’s initially at rest. The blocks then collide and stick together, conserving momentum because they form an isolated system:
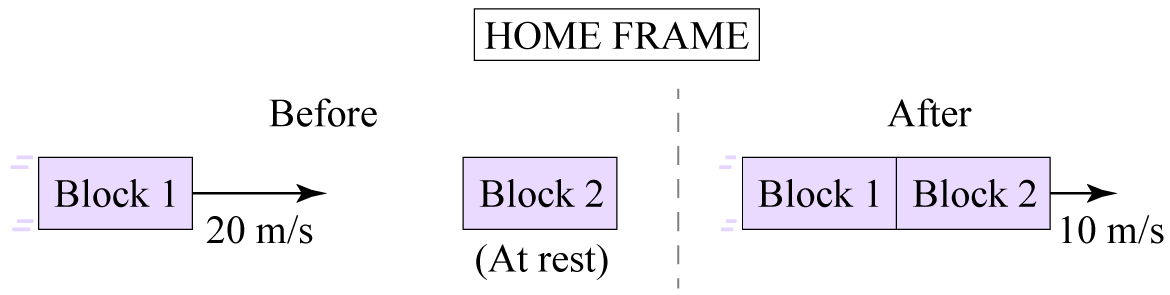
This view of the collision is from what I’ll call the “Home” reference frame. Because the initial momentum of the system is 20 kg m/s and momentum is conserved, the final velocity of the combined 2-kg block must be exactly 10 m/s.
Now let’s view this same collision from what I’ll call the “Other” reference frame, which is moving to the right at exactly 10 m/s with respect to the Home frame. In the Other frame the final velocity of the combined blocks is zero, while the initial velocity of Block 2 is exactly −10 m/s:
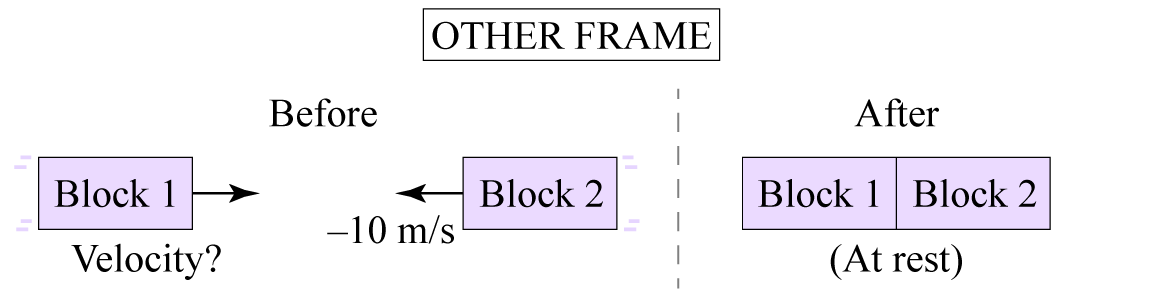
But what’s the initial velocity of Block 1? If we didn’t know about relativity we would simply subtract 10 m/s (the Other frame’s velocity) from 20 m/s (Block 1’s velocity in the Home frame) to obtain 10 m/s. But the Einstein velocity transformation tells us that this isn’t exactly right. For if we work backwards, combining the 10 m/s velocity of the block in the Other frame with the 10 m/s velocity of the Other frame with respect to the Home frame, we would get a value very slightly less than 20 m/s for the block’s velocity back in the Home frame. In order for this velocity to come out to exactly 20 m/s, the velocity of Block 1 with respect to the Other frame must instead be very slightly greater than 10 m/s.
And now we have a problem: As viewed from the Other frame, the final momentum of this system is exactly zero but the initial momentum is not; in fact it is slightly positive. By assuming that momentum was conserved in the Home frame, I’ve proved that momentum is not conserved in the Other frame. Momentum conservation is therefore incompatible with the principle of relativity, which requires that the laws of physics are valid in all inertial reference frames.
So what do we do? One option would be to simply give up, and conclude that momentum conservation isn’t a law of physics after all. That’s conceivable, but it would be a sad outcome and it wouldn’t explain why momentum conservation works so well at low speeds.
To make the discrepancy more dramatic, consider the collision example above but multiply all the speeds by $10^7$, so Block 1 is initially moving at 200,000,000 m/s (2/3 the speed of light), and the blocks’ final speed is 100,000,000 m/s (1/3 the speed of light). (Try to ignore the absurdity of two “blocks” simply sticking together after such a violent collision!) If the Other frame is again moving along with the blocks after the collision, what is the initial speed of Block 1 in the Other frame, according to the Einstein velocity transformation rule? What is the system’s initial (Newtonian) momentum in the Other frame?
Fortunately, there’s another option: Modify the definition of momentum! Perhaps the formula we’re using for momentum is only approximately correct—accurate enough at low speeds, but inaccurate at higher speeds.
And what is our definition, exactly? Well, it’s mass times velocity, for instance,
\begin{equation} p_x = mv_x = m\frac{dx}{dt}\qquad \text{(old definition)}. \end{equation}In Newtonian mechanics, this formula defines a perfectly good vector component because $x$ itself is a valid vector component, while $m$ and $dt$ are scalars, that is, numbers that are the same in all coordinate systems. (The quantity $dx$ is basically the difference between two $x$ values, final minus initial, but subtraction of vectors works component-wise, so this subtraction doesn’t affect the status of the expression as a valid vector component.)
And now, perhaps, you can see the issue: In four-dimensional relativistic spacetime, the denominator $dt$ is no longer a scalar because it is a coordinate time interval, different in different reference frames. But there’s a straightforward fix! Instead of putting the coordinate time difference in the denominator, we can use the proper time difference $d\tau$ (which for infinitesimal time intervals is the same as the spacetime interval $ds$). This is the time interval as measured by the particle’s own clock, so it is a true scalar quantity, independent of any reference frame. Our new definition of momentum is therefore
\begin{equation} p_x = m\frac{dx}{d\tau} = \gamma m \frac{dx}{dt}\qquad \text{(new definition)}, \end{equation}where in the final expression I’ve used the metric equation to relate $d\tau$ to $dt$:
\begin{equation} d\tau = dt\sqrt{1-(v/c)^2} = \frac{dt}{\gamma}. \end{equation}The Lorentz factor $\gamma$ is very close to 1 at low speeds, which is why we never notice that we need it in everyday situations. But at speeds close to the speed of light, the extra factor of $\gamma$ in the definition of momentum makes a big difference.
In three spatial dimensions, by the way, the Lorentz factor depends on all three components of the velocity:
\begin{equation} \frac1{\gamma} = \sqrt{1-(v_x^2+v_y^2+v_z^2)/c^2}. \end{equation}Surprisingly, this implies that the $x$ component of a particle’s momentum depends on all three components of its velocity! Meanwhile, the momentum vector also has $y$ and $z$ components,
\begin{equation} p_y = m\frac{dy}{d\tau} = \gamma m\frac{dy}{dt}, \qquad p_z = m\frac{dz}{d\tau} = \gamma m\frac{dz}{dt}, \end{equation}each of which also depends, through $\gamma$, on all three velocity components.
How fast would an object need to be moving for its relativistic momentum ($m\,dx/d\tau$) to exceed its Newtonian momentum ($m\,dx/dt$) by one percent? Express your answer as a fraction of the speed of light and also in meters per second.
But wait a minute: Vectors in spacetime are supposed to have not just three components but four. That’s because in spacetime we’re allowed not only to rotate our $x$, $y$, and $z$ axes, mixing the three spatial components of any vector, but also to boost to a different inertial reference frame, mixing the time component of any vector with its space components. So if momentum conservation is to be a true law of physics, valid in all inertial reference frames, the momentum vector must also have a time component and this time component must also be conserved. And what is that time component? It must be related to $dt$ in the same way that the space components are related to $dx$, $dy$, and $dz$:
\begin{equation} p_t = m\frac{dt}{d\tau} = \gamma m \frac{dt}{dt} = \gamma m = \frac{m}{\sqrt{1-(v/c)^2}}. \end{equation}For a particle at rest, this quantity is simply the mass $m$. And we normally think of mass as a conserved quantity, so that’s a good sign! For a particle in motion, the quantity $p_t$ is greater than the mass, by an amount that depends on the particle’s speed but not on its direction of motion. It’s a lot greater at speeds close to $c$, but at much lower speeds it’s only a little greater.
To better understand this quantity $p_t$, I’d like to simplify its formula in the familiar limit of low speeds, $v\ll c$. In this limit we can use a handy formula called the binomial approximation, which says that 1 plus something small, all raised to some power, is equal to 1 plus the product of the power times the small thing:
\begin{equation} (1+\epsilon)^n \approx 1+n\epsilon \qquad \text{when $|n\epsilon|\ll 1$}. \end{equation}(If you’re not already familiar with this approximation, please add it to your mathematical toolbox. It’s incredibly useful not just in relativity but in many branches of science and engineering.) To apply the binomial approximation to the formula for $p_t$, I want to identify $\epsilon$ as $-(v/c)^2$ and identify $n$ as $-1/2$. Then for $v\ll c$ I can approximate
\begin{align} \gamma &= \biggl(1-\Bigl(\frac{v}{c}\Bigr)^{\!2}\biggr)^{\!-1/2}\nonumber \\ &\approx 1 + \Bigl(-\frac12\Bigr)\Bigl(-\frac{v^2}{c^2}\Bigr)=1+\frac{v^2}{2c^2} \qquad \text{(when $v\ll c$)}. \end{align}So at low speeds, the time component of the momentum four-vector is approximately equal to the mass, plus a small correction term that’s starting to look a lot like kinetic energy (another conserved quantity!). There’s an extra factor of $c^2$ in the denominator, but an overall constant factor won’t affect whether this quantity is conserved.
What we therefore do is multiply $p_t$ by $c^2$, and refer to this quantity as simply $E$, the relativistic energy of the particle:
\begin{align} E &= p_t c^2 = \gamma m c^2 \qquad\ \text{(at any $v$)} \\[4px] &\approx mc^2 + \frac12 mv^2 \qquad \text{(when $v\ll c$)}. \end{align}For the special case of a particle at rest, we have simply $E = mc^2$ (an equation that you may have seen before); this quantity is called the rest energy of the particle. At low speeds, a particle’s total energy is its rest energy plus the familiar Newtonian formula for kinetic energy (to a good approximation). And at high speeds, we can compute its total energy from the exact formula $\gamma mc^2$, and we define the kinetic energy to be the amount by which this exceeds the rest energy:
\begin{equation} \text{Kinetic energy} = E - mc^2 \qquad \text{(at any $v$)}. \end{equation}In any case, the relativistic energy must be a conserved quantity—and it’s the total energy that’s conserved, not the rest energy or kinetic energy separately.
Calculate $\gamma$ for $v/c$ equal to 0.1, 0.01, and 0.001. Compare each value to what you get using the binomial approximation, and comment on the results.
Let me now summarize this remarkable story. First I showed that the old Newtonian definition of momentum is incompatible with the principle of relativity. To fix this problem, I suggested a modification to the definition of momentum that seems to have the desired vector properties. But if momentum conservation is to be a true law of physics, valid in all inertial reference frames, then the momentum vector can’t have just three components; it must also have a time component, which must also be conserved. Finally, I showed that this time component is closely related to the familiar concepts of mass and energy. I inserted a factor of $c^2$ to give it the right units, and arrived at the relativistic version of energy conservation.
The implications of relativistic energy conservation are plentiful and astounding.
For an object at rest, the equation $E=mc^2$ tells us that the mass of any object is effectively a measure of its total energy content; the factor of $c^2$ merely converts between mass units and energy units. But look at the numbers! A 1-kg object at rest has a total energy of
\begin{equation} E = (1~\textrm{kg})(3\times10^8~\textrm{m/s})^2 = 9\times10^{16}~\textrm{J}, \end{equation}or a little over 20 megatons (of TNT explosive equivalent). It’s probably a good thing that nobody knows a quick and practical way to convert all this energy to other forms!
Speaking of explosives, a typical combustion reaction releases about $10^7$ joules of energy for every kilogram of reacting chemicals. To pick a specific number, when hydrogen and oxygen burn to form water, the energy released (usually as heat to the surroundings) is about 16 MJ per kilogram. This might sound like a lot of energy, but it’s nothing compared to the rest energy, which is again nearly $10^{17}$ joules. In principle we could weigh the hydrogen and oxygen gases before the reaction, then weigh the cooled-off water after the heat has dissipated, and the difference, times $c^2$, should equal 16 MJ (for one kilogram of reactants). In practice, nobody has ever made a balance accurate enough to measure such tiny mass differences (roughly one part in $10^{10}$).
Where we can measure these mass differences is in reactions of individual atomic nuclei and subnuclear particles—because these reactions tend to convert much larger fractions of the total energy from one form to another. The exercises below give several examples.
Many reactions in nuclear and particle physics involve high-energy particles of light, called photons (also called gamma rays). Naturally these particles travel at the speed of light. But you might be puzzled by the fact that the Lorentz factor $\gamma$ (coincidentally the same symbol to denote a $\gamma$ ray) is infinite when $v=c$, apparently implying that every photon carries infinite momentum and energy. That’s not the case, and the only way to reconcile the facts with the formula is if every photon has zero mass. Then the product $\gamma m$ becomes ambiguous (infinity times zero) for photons in all the formulas above, and those formulas become merely useless for photons, not contradictory. In fact, a photon can have any amount of energy and any momentum vector, though these two quantities are related. To see how, consider the ratio
\begin{equation} \frac{p_x}{E} = \frac{\gamma m v_x}{\gamma m c^2} = \frac{v_x}{c^2}, \end{equation}in which $\gamma$ and $m$ both cancel out. This relation works just as well for a photon as for any other object. If the photon is moving in the $+x$ direction then $v_x=c$, so this ratio is simply $1/c$, implying $E=p_x c$. (One can also derive this energy-momentum relation for light using Maxwell’s equations, but that derivation is much more difficult.)
If, on the other hand, a particle has a nonzero mass, then the formula $E=\gamma mc^2$ implies that we would have to give it an infinite amount of energy to accelerate it up to the speed of light. This is another way of understanding the cosmic speed limit.
Several of the exercises below involve decays and other reactions of subatomic particles, so I’ve gathered the relevant masses and rest energies into the following table. Note that in atomic and nuclear physics it is common to measure masses in atomic mass units, also called daltons (abbreviated u or Da), where 1 u is the approximate mass of a proton or neutron, and is defined as exactly 1/12 the mass of a carbon-12 atom. It is also customary to measure energies in electron-volts (eV), where 1 eV is the energy that a one-volt battery gives to each electron it pushes around a circuit, $1.60\times10^{-19}$ joules. The table gives rest energies in MeV, where M (mega) is the metric prefix for $10^6$. For comparison I’ve also included masses in kilograms.
| Particle | Symbol | Mass (kg) | Mass (u) | $mc^2$ (MeV) |
| Photon | $\gamma$ | $0$ | $0$ | $0$ |
| Neutrino | $\nu$ | ${\sim}0$ | ${\sim}0$ | ${\sim}0$ |
| Electron/positron | $e^\mp$ or $\beta^\mp$ | $9.11\times10^{-31}$ | $0.00055$ | $0.51$ |
| Muon | $\mu^\pm$ | $1.88\times10^{-28}$ | $0.11343$ | $105.66$ |
| Pion (neutral) | $\pi^0$ | $2.41\times10^{-28}$ | $0.14490$ | $134.98$ |
| Pion (charged) | $\pi^\pm$ | $2.49\times10^{-28}$ | $0.14983$ | $139.57$ |
| Proton | $p$ | $1.67\times10^{-27}$ | $1.00728$ | $938.27$ |
| Neutron | $n$ | $1.67\times10^{-27}$ | $1.00866$ | $939.57$ |
| Alpha ($^4$He nucleus) | $\alpha$ | $6.64\times10^{-27}$ | $4.00151$ | $3727.38$ |
Estimate the mass increase of a cup of tea as its temperature increases from room temperature to the boiling point. (It takes 4.2 J of energy to raise each gram of water by one degree Celsius.)
Although the metric equation is good news for space travelers who wish to reach distant stars within a human lifetime, the energy requirements pose a challenge. Suppose, for instance, that you wish to take a trip on a starship that travels at 4/5 the speed of light. If you and your luggage have a combined mass of 100 kg, how much kinetic energy must you (including your luggage) acquire to reach cruising speed? Convert your answer to kilowatt-hours (kWh), then look up the current per-kWh cost of electrical energy in your area. Use these numbers to estimate the cost of a ticket on this starship. Discuss the assumptions behind your estimate, and the practicality of interstellar travel.
The sun has a mass of $2\times10^{30}$ kg and radiates energy at a rate of about $4\times10^{26}$ watts. How much mass does the sun lose in each second? At the rate it’s going, how long would it take the sun to lose one percent of its mass?
Starting from Avogadro’s number $6.022\times10^{23}$, determine the number of kilograms in one atomic mass unit (to four significant figures). Use this conversion factor to check a couple of the entries in the Particle Masses and Rest Energies table above. Then calculate the rest energy in MeV of a hypothetical particle whose mass is exactly 1 u, and use this conversion factor to check a couple of the entries in the table.
Technetium-99m ($^{99\textrm{m}}\textrm{Tc}$) is an excited, metastable state of the isotope technetium-99 that is commonly used in diagnostic medical procedures. It spontaneously decays to ordinary $^{99}\textrm{Tc}$ with a half-life of 6 hours, emitting a photon (gamma ray) with energy 0.140 MeV. By about what fraction does the mass of the technetium nucleus (or atom) decrease when it loses this energy? (Hint: The atomic mass number 99 tells you that a mole of $^{99}\textrm{Tc}$ has a mass of 99 grams, where a mole equals $6\times10^{23}$ atoms. The kinetic energy of the recoiling Tc nucleus is negligible, but it’s a nice exercise to verify this using momentum conservation.)
An alpha particle, or helium-4 nucleus, consists of two protons plus two neutrons, held together by the strong nuclear force. Notice from the table above that its mass is somewhat less than the total mass of its constituent protons and neutrons. How much energy would you need to provide, in MeV, in order to separate these constituents from each other? (This quantity is called the binding energy of the nucleus.) What is the binding energy as a fraction of the alpha particle’s rest energy?
A uranium-238 nucleus decays (into thorium-234, with a half-life of 4.5 billion years) by emitting an alpha particle. If the uranium nucleus is initially at rest, then the alpha particle comes out at a speed of $1.42\times10^7$ m/s. (a) Calculate the kinetic energy of the emitted alpha particle in MeV. How accurate is the nonrelativistic formula $K = \frac12 mv^2$? (b) To conserve momentum, the thorium nucleus must recoil as the alpha particle is emitted. What is its recoil speed? (c) What fraction of the rest energy of the uranium nucleus is converted into kinetic energy by this decay?
A free neutron (not bound inside a nucleus) is unstable, decaying with a half-life of about 10 minutes into a proton, an electron, and a neutrino (technically an antineutrino, but the distinction doesn’t matter here): $$ n \longrightarrow p + e^- + \nu. $$ Referring to the table for the needed mass data, determine the total kinetic energy of the products of this decay. What fraction of the neutron’s rest energy is this?
The nuclear fusion reaction that powers our sun combines four protons and two electrons to form a helium nucleus, also called an alpha particle, along with several photons and neutrinos: $$ 4p + 2e^- \longrightarrow \alpha + \text{photons} + \text{neutrinos}. $$ What is the net gain in kinetic energy during this reaction? What fraction of the reactants’ rest energy is converted to kinetic energy? (Refer to the table for the needed mass data.)
The neutral pion has a very short half-life of less than $10^{-16}$ seconds. It normally decays into a pair of photons (gamma rays). What are the energies of these photons, assuming that the pion is initially at rest? Why is it impossible for a neutral pion to decay into a single photon?
The positron is the electron’s so-called antiparticle, with the same mass as an electron but opposite electric charge. When a positron interacts with an electron, they can annihilate into two or more photons: $$ e^+ + e^- \longrightarrow \text{photons}. $$ (a) Prove that there must be at least two photons produced in this reaction: annihilation into a single photon is not possible. (b) If the positron and electron are initially at rest and just two photons are produced, what are the photons’ energies?
The LEP collider at the CERN laboratory in Geneva accelerated electrons and positrons to a maximum energy of 104,000 MeV (104 GeV) each. How does the energy of such a particle compare to its rest energy? What is the velocity of such a particle, expressed as a fraction of $c$? (Hint: Solve for $v/c$ in terms of $\gamma$ and then use the binomial expansion to determine the amount by which $v/c$ differs from 1.)
Often an object’s energy and momentum are of more interest to us than its velocity, so we want an equation that relates energy to momentum and mass, with velocity eliminated. Show that for any object, this relation is $$ E^2 - |\vec p c|^2 = (mc^2)^2, $$ where $\vec p$ represents the three spatial components of the momentum. Like the metric equation, this equation tells us to subtract the squares of the three spatial components of a four-vector from the square of its time component, resulting in a quantity that is frame-independent (a so-called Lorentz scalar). What does this equation tell us about a massless particle such as the photon?
A charged pion usually decays (with a half-life of 18 ns) into a muon plus a neutrino. Use both energy and momentum conservation to determine the neutrino’s energy and the muon’s kinetic energy. (Hint: Use the energy-momentum-mass relation from the previous problem, rather than working with the muon’s velocity as a variable.)
A gamma-ray photon collides with a free electron that is initially at rest. This problem and the next explore some possible outcomes. (a) First use momentum and energy conservation to prove that the electron cannot simply absorb the photon (a reaction we would write as $e^- + \gamma \longrightarrow e^-$). This means that the simplest possible reaction is $e^- + \gamma \longrightarrow e^- + \gamma$, with a single photon in the final state; this reaction is called Compton scattering. (b) Suppose that the Compton-scattered photon comes straight back, opposite to the initial photon’s direction of motion, while the electron recoils in the initial photon’s direction. Use relativistic momentum and energy conservation to derive a formula for the final photon energy in terms of the initial photon energy and the electron’s rest energy $mc^2$. (c) Discuss what happens in the limiting cases where the initial photon’s energy is much less than and much greater than the electron’s rest energy.
Repeat part (b) of the previous problem for the general case in which the final photon’s direction makes an angle $\theta$ with the initial photon’s direction. Now there are two nontrivial momentum components, which are separately conserved. You should obtain the Compton formula, $$ \frac1{E_f} = \frac1{E_i}+\frac1{mc^2}(1-\cos\theta), $$ where $E_i$ and $E_f$ are the initial and final photon energies, respectively. Discuss the predictions of this formula for some interesting values of $\theta$ and $E_i/mc^2$.
Let’s return to the thought experiment of the two colliding blocks, at the beginning of this lesson. In that example I assumed not only that momentum is given by the Newtonian formula $m\vec v$, but also that we could simply add the masses of the two blocks to obtain the mass of the final, combined block. Now we know better: The kinetic energy lost in the collision is converted to thermal energy, which adds to the mass of the combined block. If we take the final mass and the final velocity to be our two unknowns, then we need two equations to determine these two unknowns.
(a) It’s easier to work algebraically at first, so let each initial block have mass $m$ and let $v_0$ be the initial velocity of Block 1, with Block 2 initially at rest. Assuming that the two blocks stick together and that all energy remains in the combined block, write the two equations that express momentum and energy conservation. Combine these equations to eliminate the final mass and obtain an expression for the final velocity in terms of $v_0$.
(b) Low speeds like 20 m/s make relativistic effects hard to discern. So evaluate the final velocity numerically (to three or four decimal places) for $v_0/c=2/3$. (Try to ignore the absurdity of two “blocks” sticking together in such a violent collision!) Also evaluate the final mass in this case, as a numerical multiple of the initial mass. Comment on your results.
(c) Now imagine viewing this collision from the reference frame in which the total momentum is zero. Sketch the initial and final configurations in this frame. What is the initial velocity of Block 2 in this frame? If momentum is to be conserved in this frame, what must be the initial velocity of Block 1? Finally, use the Einstein velocity transformation formula to transform Block 1’s initial velocity back to the original reference frame, to check that everything is consistent. Explain the significance of this consistency in your own words.
This concludes this abbreviated introduction to special relativity. If you would like to learn more about special relativity, I highly recommend the following three texts. All are at about the same level as these lessons but provide more detail, and all make frequent use of spacetime diagrams, as I have:
If you would like to see special relativity applied and extended in the context of electromagnetism or gravity, here are some treatments of those subjects that I recommend:
Copyright ©2022 by Daniel V. Schroeder. This work is licensed under a Creative Commons Attribution 4.0 International License. (This copyright and license do not apply to illustrations attributed to another source.)
Click here to download a zip archive of the original vector-graphic illustrations. I recommend starting from these if you wish to adapt or translate an illustration.
I typed this HTML document directly into a text editor (BBEdit). The source file is human-readable, so you can use your browser’s View Source or Page Source command to see the (minimal) styling code. MathJax is typesetting the equations. I created the illustrations in Adobe Illustrator, then exported them in png format at double the (nominal) displayed resolution for sharpness on high-resolution displays. To label the illustrations I used LaTeXiT (included in the MacTeX distribution), exporting the output as pdf with outlined fonts.