
The purpose of this talk is not to present anything new. Instead I'd simply like to encourage you to consider taking an approach to teaching electrodynamics that was introduced in the 1960's by Edward M. Purcell in his well-known book, Electricity and Magnetism, in the Berkeley Series of introductory physics texts. Specifically, Purcell in his book used relativity to essentially derive the existence of magnetic forces and of electromagnetic radiation. His approach brings these subjects to life in a way that doesn't require a lot of math.
After a few introductory comments and disclaimers, I'll review Purcell's ideas and thus try to convince you to try this approach yourselves. The two ideas are first, that magnetism is a consequence of length contraction, and second, that electromagnetic radiation happens because of the cosmic speed limit, that is, because information can't travel faster than the speed of light.
Before starting I have to put in a bunch of disclaimers:
So let's start with Purcell's basic explanation of magnetic forces. Shown below is a model of a wire with a current flowing to the right. To avoid minus signs I'm taking the current to consist of a flow of positive charges, separated by an average distance of l. The wire has to be electrically neutral in the lab frame, so there must be a bunch of negative charges, at rest, separated by the same average distance. Therefore there's no electrostatic force on a test charge Q outside the wire. What happens, though, if the test charge is moving to the right? For simplicity, let's say its velocity is the same as that of the moving charges in the wire. Now consider how all this looks in the reference frame of the test charge, where it's at rest. Here it's the negative charges in the wire that are moving to the left. Because they're moving, the average distance between them is length-contracted by the Lorentz factor. Meanwhile the positive charges are now at rest, so the average distance between them is un-length-contracted by the Lorentz factor. Both of these effects give the wire a net negative charge, so it exerts an attractive electrostatic force on the test charge. Back in the lab frame, we call this force a magnetic force.

By the way, it's remarkable that we can measure magnetic forces at all, since the average drift velocity in a household wire is only a snail's pace: v/c is typically only 10-13, so the Lorentz factor differs from 1 only by about one part in 1026. We can still measure this effect because the total charge of all the conduction electrons in a meter-long wire is tens of thousands of coulombs; two such charges separated by only a few millimeters would exert enormous electrostatic forces on each other.
You can repeat the preceding calculation for the more complicated case where the test charge's velocity differs from the average drift velocity of the charge carriers in the wire. Their velocities can also be opposite in direction. In each case, you still get the correct expression for the magnetic force on the test charge. The case where the test charge moves perpendicular to the wire is still more complicated, but we can understand it qualitatively after digressing to consider how electrostatic fields transform from one reference frame to another.
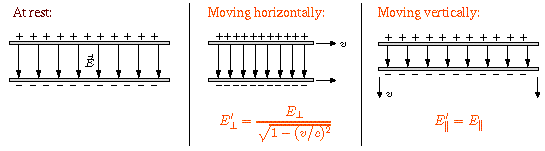
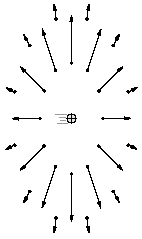
Now consider the electrostatic field of a point charge at rest, shown at left below. At every point on the circle (actually a sphere), the field has the same strength and points directly away from the particle.
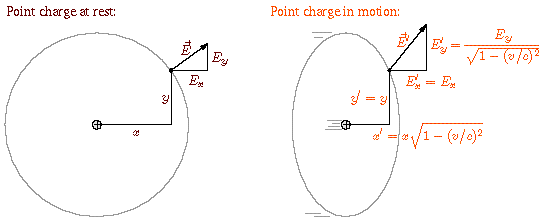
If we put this system in motion to the right (shown at right), two things happen. The first is that the sphere gets length-contracted, flattened in the direction of motion. The second is that the components of the field perpendicular to the motion get stretched by the very same Lorentz factor. Therefore the field still points directly away from the point charge, but it's not the same in all directions: it's weaker in front of and behind the particle, and stronger to the sides, as shown below.
With all this in mind, let's now consider our wire again, but with the test charge moving directly toward it.
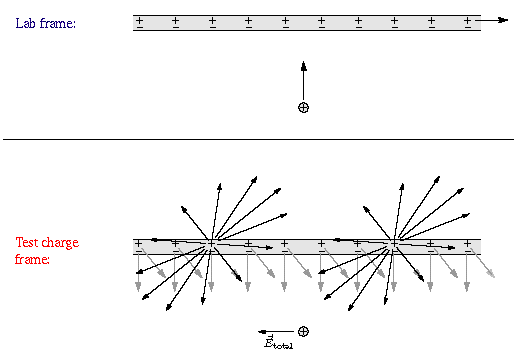
In the frame of the test charge the wire is moving downward. The negative charges in the wire, which are moving straight down, have their electric fields distorted as shown previously, but these fields are symmetrical from left to right so they exert no net horizontal force on the test charge. The positive charges in the wire, however, are now moving diagonally, so their fields are distorted as shown above. At the location of the test charge, the field of the positive charge to the right is stronger than that of the positive charge to the left, so the test charge feels a net force pushing it to the left.
In summary, we can account for the direction of the magnetic force on the test charge no matter which way it's moving, and this motivates us to introduce a magnetic field vector that points into the page, with the force given by a cross-product of v and B.
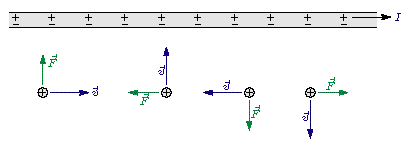
At this point in the course you can go on to various applications of magnetism. You could also introduce the Biot-Savart law and Ampere's law, but they're not really needed for most applications.
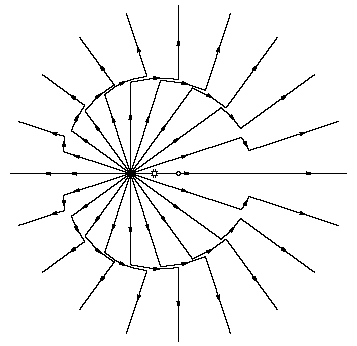
The other part of electrodynamics that I'd like to discuss is radiation. If you're familiar with Purcell's book you'll remember that he draws some beautiful illustrations of the field lines of a point charge that suddenly starts moving or comes to a sudden stop. I prefer to consider a bounce, where the particle is first moving to the right, say at 1/4 the speed of light, then bounces off a brick wall and moves back to the left at the same speed.
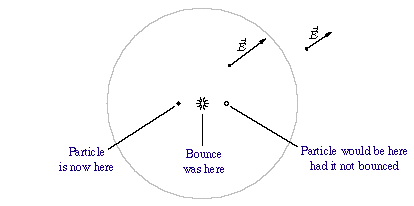
Near the particle, its electric field points directly away from where the particle actually is. But far away, the news that the bounce has occurred hasn't arrived yet, so the field points away from where the particle would be had there been no bounce. As David Griffiths likes to say, "electromagnetic news travels at the speed of light." So there's an inner region of field lines pointing away from the particle, and an outer region of field lines pointing away from the imaginary point where it would be. These two regions are separated by a transition region--a spherical shell that expands outward at the speed of light.
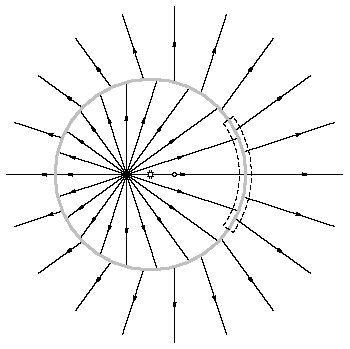
The next question is, what does the field look like in the transition region? I think most people would guess that you just connect up the corresponding field lines, and this is correct, because field lines can't start or end in empty space. To be rigorous, you can apply Gauss's law to the dashed surface shown above, and then to a more complicated surface that actually follows the field lines through the transition region. A complete sketch of the field around the bouncing point charge is shown below. Notice that the transverse field is weakest to the right and left, and strongest in the perpendicular directions. As time passes, the shell expands at the speed of light. The transverse field also gets stronger because the gap, between the particle's actual location and the point where it would be, expands.
(There exists software for drawing and animating pictures like this. An old DOS program that does this is included in the Physics Simulation Programs package available from Physics Academic Software. A somewhat prettier Macintosh program has been created by Blas Cabrera, Sha Xin Wei, and Jim Terman. This program is now in the public domain; to download it, click here.)
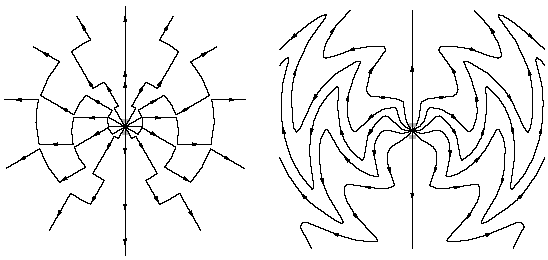
When teaching this material I always assign homework problems in which students are asked to sketch the field lines for charges undergoing various instantaneous accelerations. Shown at left below is the somewhat complicated example of a point charge bouncing vertically between two walls. If you just round off the corners, you get something like the illustration on the right, for a point charge undergoing simple harmonic motion as in a radio transmission antenna. Notice that the waves are strongest in the horizontal directions, perpendicular to the particle's acceleration.
In the original edition of his book, Purcell went no further than drawing these pictures and interpreting them qualitatively. But in his second edition he added an appendix in which he computes the radiation field quantitatively.
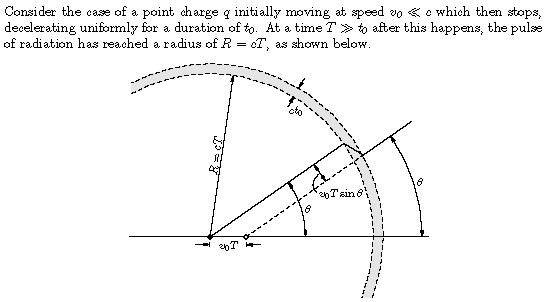
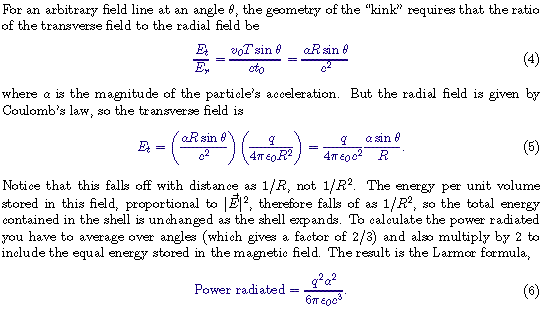
I've never understood why the Larmor formula isn't even mentioned in most introductory textbooks. In fact I never saw it in all of my undergraduate education. Yet it's simple to interpret, and it has all sorts of interesting uses. I've already mentioned antennas. You can also understand why the sky is blue and polarized, and explain why a classical Rutherford atom, with electrons orbiting around the nucleus, would be unstable, radiating away all its energy in a fraction of a nanosecond. More generally, the Larmor formula ties electromagnetic waves to their source, making it clear that radiation requires not just motion, but also acceleration of charged particles. Once you have the Larmor formula, why bother to cover Maxwell's equations?
Last modified on September 22, 1999.