 |
|
| Orbital Characteristics of Spectroscopic Binaries
|
To investigate the effect that changes in mass, separation, eccentricity, and inclination angle have on the characteristics of the radial velocity curves of a spectroscopic binary.
The most important property of a star is its mass, but stellar masses are much harder to measure than luminosities or surface temperatures. The most dependable method for "weighing" a star relies on Newton's version of Kepler's third law (see your text). This law allows us to calculate the masses of orbiting objects by measuring both the period and average distance (semimajor axis) of their orbit. We must be able to determine the orbital properties of the two stars in order to derive the masses and radii of the system.
There are three main classes of binary systems: visual binary, eclipsing binary, and spectroscopic binary. In this exercise, we examine the characteristics of spectroscopic binaries by noting the effects changes in mass, separation, eccentricity, and inclination angle have on the shapes of the radial velocity curves and the Doppler shifts of the lines in their spectra.
We detect spectroscopic binary systems by observing Doppler shifts in the spectral lines. If one star is orbiting another, it periodically moves toward us and away from us in its orbit, and its spectral lines show blueshifts and redshifts as a result of this motion. Each of the two stars we see when we view Mizar through a telescope is a spectroscopic binary. (Mizar is the star at the "bend" in the handle of the Big Dipper and pictured in the heading to this exercise.)
We measure the orbital period of a spectroscopic binary by noting the time it takes the spectral lines to shift back and forth. Except in rare cases, we can calculate the separation of a binary only if we know the actual orbital speeds of the stars. The primary technique for measuring stellar speeds relies on the Doppler effect, but Doppler shifts tell us only the portion of a star's velocity that is directly toward us or away from us. Orbiting stars generally do not move directly along our line of sight, so their actual velocities can be significantly greater than those we measure through the Doppler effect. The orbits of eclipsing binaries are particularly important to the study of stellar masses because we know the inclination of the system and thus can calculate the actual orbital speeds of the stars.
The simulation used for this exercise is a Java applet written by
Professor Terry Herter of Cornell University, and is used with his permission. Dr Herter describes his program as follows:
Allows you to set the masses, orbital separation, orbital eccentricity,the inclination angle to our line of sight, and the angle of thenodes of an orbiting star pair. You see the privileged (from abovethe orbit) and the Earth view of the system (which depends onthe inclination angle). The observed velocities of the two stars,and the Doppler shifted spectral lines (as seen against the combinedcontinuum from the two stars) are also shown in the upper rightbox. The spectral lines associated with each star are indicatedand the unshifted line positions are also marked. The movementof the spectral lines against the continuum has been greatly exaggeratedfor display purposes, and the difference in brightness of thetwo stars has been ignored.
Note: To run these simulations you will need a JAVA enabled Web browser, such as Netscape 2.02 or 3 or Internet Explorer for the PC and Netscape 3.0 for the Mac.
Spectroscopic Binary Simulation
Take a look at the image to the right of each of the following definitions and find the corresponding parameters on the simulation:
| M1 or M2 | The mass of each of the two stars. | 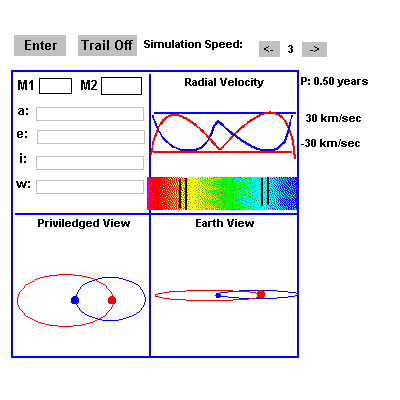 |
|---|---|---|
| Separation a: | The distance between the two stars in solar radii. | |
| Eccentricity e: |
Eccentricity of the orbit | |
| Inclination angle i: | Angle of the orbital plane of the stars to
our line-of-sight. 0o - face on 90o - edge on Opposite from standard. |
|
| Node angle w: (ignore) | Angle of the major axis as measured in the orbital plane |
Do some trial investigation to see how you can adjust each of the parameters for the simulation:
Adjust each of the star parameters -- masses, separation, eccentricity, or inclination (ignore w:).
Click "enter" to update the simulation parameters.
Use "pause" to start and stop the simulation, if desired.
If the picture is messed up at anytime, use "enter"to redraw it.
The number between the "<=" and "=>"buttons, is the rough time (in seconds) it takes the simulation to complete an orbit. Make this number larger or smaller by clicking the "arrow" buttons.
Print a copy of Table 1 and fill in the appropriate columns for the changes given for Models 1 - 12. Make sure you "refresh the screen" after each change, and click on "enter" to activate the changes.
How close were your predictions for the period and velocity range for the increase in the mass of M1 from 6 to 12?
Based on what you know about the effects of an increase in gravity, do these results seem logical? Explain.
How close were your predictions for the period and velocity range for the increase in the separation a from 0.4 to 2.0 solar radii?
Based on what you know about the effects of a decrease in gravity, do these results seem logical? Explain.
Compare Model 5 to Model 6. What did you find most interesting when you changed the eccentricity e from 0.0 to 0.9?
Where in their orbits are the stars moving the fastest?
Where in the orbits of the stars do the absorption lines shift the
most? Connect your answer here to your answer for the previous question.
Take a look at the Earth view for the effects for Model 7, i = 90.0. What might we see for a star with this set-up? Why is this important to astronomers?
Take a look at the effects your parameter changes had in Model 8. Would we ever detect this binary spectroscopically?
Take a look at the effects your parameter changes had in Model 9. Would we ever detect this binary spectroscopically? Justify your answers to this question and the previous question.
Play around by changing the values of the parameters. Be sure,however, to only change one at a time to see what effect it hason the motion of the stars and the velocities we see. Summarize the results for one of your simulations here.