---

Summary

The student will use CCD images of the Crab Nebula, a Hubble Space Telescope image of SN1987a, and a CCD image of supernova 1993j to examine a number of characteristics of supernovae and their remnants.

Background and Theory

Supernova explosions are the most powerful events in the Universe. In less than a second, about 10⁴⁴ Joules of energy are released---about the same as the Sun has released in its entire lifetime! The explosion results from the death of a massive star which has consumed its entire fuel supply. The apparent magnitude of a supernova brightens by about 10 magnitudes within a few hours, and for a few months the luminosity of the star is comparable to the luminosity of the entire parent galaxy.

Supernovae are rare events, occuring only once or twice per century in a typical galaxy. Thre have been just six supernovae seen in the Milky Way in recorded history, with the most recent occuring in 1604, just before the advent of telescopes. The perceptive reader will notice that this rate is much less than the rate of one or two per century reported above (which gives ~20-40 in 2000 years). At visible wavelengths, we cannot see very far into the disk of our galaxy due to light extinction by dust. Therefore, a supernova must be quite close (within ~4 parsecs) to be observed. The 1-2 per century rate is based on average detection rates in galaxies other than our own in which we can see the galactic disk face-on with little extinction.

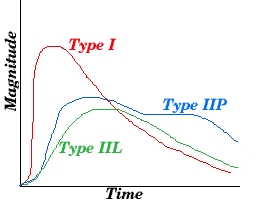
Supernovae are classified into two broad categories, based on their light curves (brightness vs. time). Type I supernovae rise sharply to a maximum, and decay gradually, whereas Type II supernovae rise and decay more gradually. Type II can be sub-divided into IIL (linear decay) and IIP (plateau decay). The figure below is a sketch of the three types of light curves.

The spectra of the two main types of supernovae also differ. Type II spectra show mostly hydrogen lines, while Type I spectra have lines of many elements. The progenitor star of a Type I supernova is thought to be a Population II white dwarf in a binary system with a red giant companion. Mass from the red giant accretes onto the white dwarf until the dwarf's mass passes the Chandresekhar limit of 1.4 solar masses. The dwarf then collapses violently and becomes a Type I supernova. The progenitor star for a Type II supernova is thought to be a Population I massive red (or blue) supergiant. After the star ceases nuclear fusion, gravity takes over and compresses the star to a very small diameter. This implosion causes a shock which bounces off the core, resulting in an explosion which we see as a Type II supernova. The shock carries of a large fraction of the stellar atmosphere at speeds of 13,000-30,000 km/s.

In this exercise, you will study two supernovae:

• The Crab supernova (SN1054 in Taurus) is probably the most well-known and best studied of all supernovae. It resulted from a stellar explosion in 1054 A.D. and was widely reported in the historical records of Chinese and Japanese court astronomers. Although the explosion took place about 2000 pc away, it was visible for about a month in the daytime sky. Even today the Crab supernova remnant is the brightest object in the sky at X-ray wavelengths. Optically it is fairly dim (V~10), but it is a beautiful object when imaged with large telescopes.
• Supernova SN1987a was the first 'nearby' supernova to be observed since the invention of the telescope. It occurred 50 kpc away, in the Large Magellanic Cloud. At peak brightness, it reached 2nd magnitude, and was featured on the cover of Time magazine. This supernova was only visible from the Southern Hemisphere.

Procedure
Part A: The expansion speed of the Crab Supernova Remnant

1. Measure the average radius of the Crab Supernova Remnant in pixels.
2. The pixels in the image have an angular size of 1.2 arcseconds per pixel. Convert the radius of the Crab to arcseconds. This is the angular size, a.
3. The distance, D, to the Crab SNR is about 2000 pc. You can use the small angle formula:
   d=(D*a)/206265"
   to find the actual size, d, of the Crab in pc. Convert this size to A.U., then to kilometers.
4. Assume that the expansion speed of the remnant has been constant since it was formed. You can calculate the expansion speed of the remnant by dividing the radius of the nebula in km by the age in hours. Compare this speed to other speeds you know, such as the speed of a car on the highway (~120 km/hr).

Part B: SN1987a

1. In this image taken by Hubble Space Telescope, you can see the supernova 1987a. This image was taken prior to the repair mission in 1993. You can see two bright stars, plus a third surrounded by a ring of material. This ring was shed from the outer layers of the blue supergiant star Sanduleak -69 202 millions of years prior to the supernova explosion, as the star evolved from a red supergiant.
   

2. Measure the true linear diameter of the ring (in pixels). Be sure to measure at the widest part of the ring, since it is actually circular, and you are viewing at an angle.
3. Convert this linear diameter to an angular size by multiplying by the image scale (0.025 arcseconds/pixel).
4. Use the small angle formula (above) to find the actual size of the ring in kilometers. The distance, D, to the ring is about 50,000 pc.
5. Assuming that the ring was shed at a velocity of about 20 km/s, as is typical of red supergiant winds, how long ago was this ring shed from the central star? (Don't forget to use the radius instead of the diameter for this calculation!)
6. From the ratio of the smallest to the largest widths of the ring, estimate its inclination to our line of sight, i.
   i=sin^-1(smallest/largest)

7. The shock wave itself is not luminous enough to be seen optically in this image. Ultraviolet spectroscopy was used shortly after the explosion to detect carbon IV transition lines. The rest wavelength, l₀, of carbon IV is 190.4 nm. The carbon IV line in this shock wave had Doppler shifts, dl, of up to 19.6 nm. Use the Doppler equation:
   v/c=dl/l₀
   to find the velocity, v, of the shock wave. Recall that c is the speed of light, equal to 3X10⁵km/s.
8. Given the speed of the shock wave and the ring's linear size which you have obtained, calculate how long it took the shock wave to reach the ring after the explosion occured. The first pictures of this collision were taken in February, 1998. How close was your estimate? What are possible sources of any discrepancy between your 'prediction', and what happened in nature?