The Sun

The Sun is a Main Sequence star and therefore derives its energy from the fusion of Hydrogen nuclei into Helium. This process, known as the p-p cycle, starts with four Hydrogen nuclei and produces one Helium nucleus, and energetic positrons, neutrinos, and gamma rays.

Four Hydrogen nuclei have a combined mass of M4H=6.693X10-27 kg, and one Helium nucleus has a mass of MHe=6.645X10-27 kg. The difference in the initial and final total mass in each fusion process, tex2html_wrap_inline87M = M4H - MHe = 0.048X10-27 kg, is converted into energy (and the Sun "loses" this mass). This is the famous tex2html_wrap_inline95, where m in this case is the difference in the masses tex2html_wrap_inline87M and c is the speed of light. The amount of energy released every time this takes place is tex2html_wrap_inline87Mc2=4.3X10-12 Joules.

Star bright: Powering the Sun

The Sun's total luminosity, 4X1026 Watts (or Joules/second)1, is ultimately derived from the energy released by many fusion reactions each second.

1. How many fusion reactions per second are required to sustain the Sun's luminosity of 4X1026 Watts?

Your answer should be roughly 100,000,000,000,000,000,000,000,000,000,000,000,000 (1038)!!

2. The Sun is losing mass each time a fusion reaction occurs. What is the rate at which the Sun's mass is decreasing (in kilograms per second)?

Your answer should be about several billion (109) kg / s. Since one ton is 103 kg, express this in millions (106) of tons per second. If one car weighs about 2 tons, how many millions of cars per second is this?

3. How many years does it take for the Sun to lose the equivalent of the Earth's mass, M =6X1024 kg? Express this number in years (there are approximately 3X107 seconds in a year).

That's a mighty long time: Lifetime of the Sun

1. Here are pretty good assumptions about the Sun:

  1. The Sun was initially composed only of pure Hydrogen;

  2. The Sun's luminosity does not change over time;

  3. The Sun will use about 10% of its initial mass in fusion reactions2;

  4. . The Sun's total mass is approximately 2X1030 kg, which hasn't changed much since the Sun formed.

Use this information to estimate how long the Sun can fuse Hydrogen into Helium.

2. We can't directly measure the age of the Sun. However, the oldest rocks found on the surfaces of the Earth and the Moon are about 4.5X109 years old. What does this tell us about the current age of the Sun? How much longer will the Sun remain on the Main Sequence?

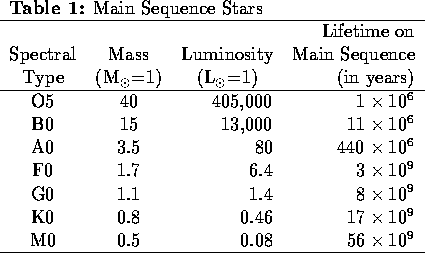
table39

3. Look at Table 1. The Sun is a G2 star. You might expect that stars more massive than the Sun will live longer than the Sun because the massive stars have more fuel available to burn: for example, a 15 Mtex2html_wrap_inline159 star should last 15 times longer than the Sun, or 150X109 years. But according to this table a 15 Mtex2html_wrap_inline159 star lasts a mere 11X106 years. Why?

4. The age of the Universe is believed to be close to 14X109 years. Which classes of stars have never left the Main Sequence? Explain.


Wed Feb 20 14:20:07 PST 2002