Introduction to Astronomy

Curvature


You remember from all of our discussion of black holes, that space is curved, locally by the presence of mass, and that gravity can be thought of simply as 'bent space'. But it's also true that the Universe as a whole could be curved. (Why not?!) Today, we are going to talk about these different possible curvatures of space (and time, but we won't really worry about time. You will see that the curvature of space is difficult to imagine, and the curvature of time is absurdly difficult to imagine, and NOBODY is really capable of it.).

There are three options for the curvature of space:
  1. Positive curvature
  2. Zero curvature (flat)
  3. Negative curvature
We'll look at each of these separately, and try to understand them by thinking about 2-dimensional analogies to each of these options. After that, you must try to 'imagine them' into three dimensions. This is very hard, and will hurt your head!

  1. Positive Curvature In 2-D, this is like the surface of a balloon. If you are confined to the surface of the balloon, so that you are a balloon creature, living in 2-D, you can go up-down, or right-left, but in-out of the balloon makes NO SENSE to you. You can't even imagine it.
    If the balloon is sufficiently large, and you are sufficiently small, it looks flat. (This is what happened to all those 'flat-Earth' people in Columbus' time. They thought the Earth was flat, because it looked that way. A person is small compared to the size of the Earth.)
    This positively curved surface has several properties. It is finite, that is, not infinite. It has no boundary (you can go around and around on a ball with out ever running into a wall), and has no center. (Think about it this way---if there is no boundary, there CAN'T be a center---you define the center of a room by looking at where the walls are.
    In a positively curved Universe, the rules of geometry are different than the ones you learned in grade school and high school. First, there are no straight lines. Any two parallel lines will converge at a point (like lines of longitude on the Earth, which are parallel at the equator, but come to a point at the North Pole). The sum of the angles of a triangle in curved space is greater than 180 degrees, and the circumference of a circle is less than 2R. By measuring these properties, a 2-D creature might be able to figure out that they lived in a positively curved, 2-D space.
    So a good description of a 3-D positively curved Universe would be that it's finite, unbounded, has no center, and is expanding (from the Hubble Law).
  2. Zero Curvature In 2-D, you want to imagine an infinite sheet of paper, extending off in all directions. A flat, 2-D space is infinite, unbounded and has no center. The geometry in a flat space is the kind of geomtry that you are used to. Parallel lines stay parallel, the angles of a triangle add up to 180 degrees, and the circumference of a circle is equal to 2R.
  3. Negative Curvature You can't even draw or imagine a 2-D negatively curved space, but on small scales, it looks like a 'Pringle'. A negatively curved space is infinite, has no boundary, and no center. Parallel lines diverge, the angles of a triangle add up to less than 180 degrees, and the circumference of a circle is less than 2R.

How might we test this?

For our Universe, the space is too big for us to use the geometrical tests, like measuring the angles of a triangle. We just can't draw triangles big enough. But we could do galaxy counts, which will tell us how the area of a circle changes with radius. To do this, you look at all the galaxies within a circle at a certain distance. If the number of galaxies changes between circles at different distances, you may be able to figure out if you are in positive or negative space, as opposed to flat. This would work in principle, but there are so many complicating factors (such as non-uniform distribution of galaxies, i.e. clusters and walls), as well as the fact that the Universe is not static, but changes over time, and looking back a certain distance is the same as looking back a certain time. So, though it would work in principle, it will not work in practice.

But, think about what we are talking about. The curvature of space. Locally, space curves in response to mass, so it makes sense to think that the density of mass in the Universe would determine the universal curvature.

If the density of the Universe is large, the Universe is positively curved.

If the density of the Universe is small, the Universe is negatively curved.

If the density of the Universe is just right, the Universe is flat.

The 'just-right' density is called the 'critical density', and is about 10-26 kg/m3; that's about 10 hydrogen atoms per meter cubed.

Astronomers define a parameter to talk about the curvature. This parameter is called 'omega nought', and is shown by 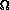0.

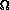0=(current density)/(critical density)

If 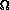0 > 1, curvature is positive.
If 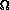0 = 1, curvature is zero.
If 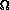0 < 1, curvature is negative.

Figuring out 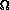0 is hard, because it includes ALL forms of energy and matter, including not only luminous matter and dark matter, but also light of all kinds, and any other kind of energy or mass that we haven't thought of yet...

Future of the Expansion

The density of the Universe also affects the future of the expansion. If the Universe is 'heavy', it will expand for a time, slow down, and then collapse. If the Universe is 'light', it will expand forever and ever. If the Universe is 'just right', it will expand for a long while, and then slow to a stop, and the Universe will remain at that density forever. These possible options are tied to the value o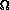f 0.

If 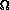0 > 1, curvature is positive, and the Universe will slow down, stop and collapse.
If 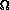0 = 1, curvature is zero, and the Universe will slow down and stop.
If 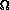0 < 1, curvature is negative, and the Universe will slow down, but continue to expand forever.

What do we think is the value of 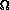0? We know that it is not VERY small, like 0.01 or less. And we know it is not VERY large, like 100 or more. Best estimates now put 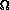0 between about 0.1 and 2. This is so close to 1 that it's hard to figure out what the curvature of the Universe and the future of the Universe will be. But we can guess about what might happen in either case.

If the Universe is positively curved, it will eventually stop expanding. So we will see the galaxies far from us slow down, and stop. Then we will observe them begin to approach (becoming blueshifted instead of redshifted). Eventually, after the more distant galaxies (which we see when they were younger), will all be approaching, and we will observe a Hubble Law in the opposite sense, with more distant galaxies approaching more quickly. As this happens, first superclusters and then clusters and then galaxies will begin to overlap. The temperature will rise from friction of all these interactions, eventually tearing apart all the matter, and sending us back to the conditions of the Big Bang. One romantic view is that the Universe will become infinitely dense, and then reexplode to form a new Universe. If this is the case, it may happen over and over again. This is sometimes referred to as 'death by fire'. The entire Universe becomes unmade in a seething, hot inferno. (Don't panic. The Universe will not reach maximum size for at least 10 billion years!)

If the Universe is negatively curved, or flat, then it will continue to grow and expand, with the density falling. There will be a sufficiently long time that galaxies will collapse into their central black holes, all the stars will burn out, and densities will not be high enough to form new stars. The black holes will eventually radiate away all of their mass, and the neutrinos, and light gradually lose energy, getting weaker (and redder in the case of light). This is sometimes called 'death by ice', and always reminds me of the end of 'The Hollow Men' by T.S. Eliot:

"This is the way the world ends;
This is the way the world ends;
This is the way the world ends;
Not with a bang, but with a whimper"

Age of Universe

The age of the universe is 1/H ONLY if the Universe has been expanding at the same rate the whole time.

If the Universe is slowing down (which it should be, because of gravity pulling stuff 'in' and slowing the expansion---think about that Virgo Cluster/Local Group interaction), then 1/H is an upper limit---the Universe can't be older than 1/H.

If the Universe is accelerating, or expanding faster all the time, then 1/H is a lower limit---the Universe must be younger than 1/H. But imagining how this could happen is very difficult, and for a long time, it has been dismissed as a possibility. Consider. In order for something to accelerate, it must be being 'pushed' outward. But all of the mechanisms that we know of 'pull' inward.

The latest evidence is that the Universe is actually accelerating. In 1998, new data were confirmed which show that the Universe used to be expanding more slowly than today! No one has yet been able to reconcile this new evidence with theory, except to say that there is 'vacuum energy', so that space itself has energy, which repels other space, accelerating it. This is a 'first-cut' explanation, and hasn't been tested in detail by enough different people to decide whether it's right or not.