
Sir Isaac Newton
The Universal Law of Gravitation
 |
Newton knew that the force which caused the apple's acceleration (gravity) must be dependent upon the mass of the apple. And since the force acting to cause the apple's downward acceleration also causes the earth's upward acceleration (Newton's third law), that force must also depend upon the mass of the earth. So for Newton, the force of gravity acting between the earth and any other object is directly proportional to the mass of the earth, directly proportional to the mass of the object, and inversely proportional to the square of the distance which separates the centers of the earth and the object.

The constant of proportionality G is known as the universal gravitational constant. It is termed a "universal constant" because it is thought to be the same at all places and all times, and thus universally characterizes the intrinsic strength of the gravitational force. The numerical value of G is very small, which is basically the reason for the force of gravity to be the weakest force of the nature. For the value of "G", refer to your text book..
But Newton's law of universal gravitation extends gravity beyond earth. Newton's
law of universal gravitation is about the universality of gravity. Newton's
place in the Gravity Hall of Fame is not due to his discovery of gravity, but
rather due to his discovery that gravitation is universal. ALL objects attract
each other with a force of gravitational attraction. Gravity is universal.
This force of gravitational attraction is directly dependent upon the masses
of both objects and inversely proportional to the square of the distance which
separates their centers.
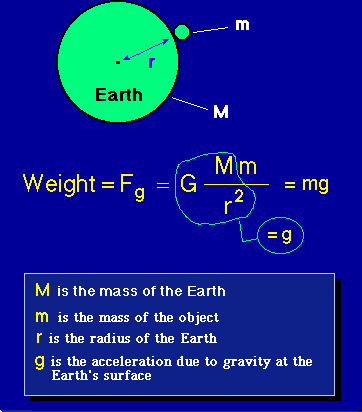
Mass is a measure of how much material is in an object, but weight is a measure of the gravitational force exerted on that material in a gravitational field; thus, mass and weight are proportional to each other, with the acceleration due to gravity as the proportionality constant. It follows that mass is constant for an object (actually this is not quite true as described by the Relativity Theory), but weight depends on the location of the object. For example, if we transported the preceding object of mass m to the surface of the Moon, the gravitational acceleration would change because the radius and mass of the Moon both differ from those of the Earth. Thus, our object has mass m both on the surface of the Earth and on the surface of the Moon, but it will weigh much less on the surface of the Moon because the gravitational acceleration there is a factor of 6 less than at the surface of the Earth.
The inverse square law proposed by Newton suggests that the force of gravity acting between any two objects is inversely proportional to the square of the separation distance between the object's centers. Altering the separation distance (r) results in an alteration in the force of gravity acting between the objects. Since the two quantities are inversely proportional, an increase in one quantity results in a decrease in the value of the other quantity. That is, an increase in the separation distance causes a decrease in the force of gravity and a decrease in the separation distance causes an increase in the force of gravity.
Furthermore, the factor by which the force of gravity is changed is the square of the factor by which the separation distance is changed. So if the separation distance is doubled (increased by a factor of 2), then the force of gravity is decreased by a factor of four (2 raised to the second power). And if the separation distance (r) is tripled (increased by a factor of 3), then the force of gravity is decreased by a factor of nine (3 raised to the second power). Thinking of the force-distance relationship in this way involves using a mathematical relationship as a guide to thinking about how an alteration in one variable effects the other variable. Equations can be more than merely recipes for algebraic problem-solving; they can be "guides to thinking."
The proportionalities expressed by Newton's universal law of gravitation is represented graphically by the following illustration. Observe how the force of gravity is directly proportional to the product of the two masses and inversely proportional to the square of the distance of separation.
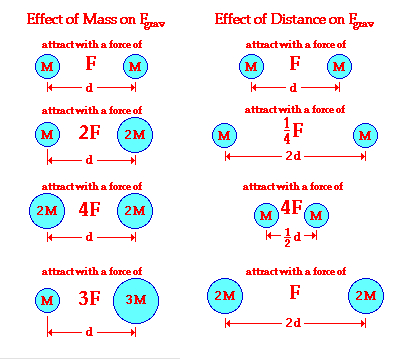
In the above figure, the figure on the left hand side indicates the effect of "mass" if the diatnce between the two objects remains fixed at a given value "d". The right hand figure shows the effect of changing the distance while keeping the mass constant, and the last part of it shows the effect of changing both the distance and the mass.
Check your understanding of the inverse square law as a guide to thinking by answering the following questions below.
Check Your Understanding
1 . Suppose that two objects attract each other with a force of 16 units (like 16 N or 16 lb). If the distance between the two objects is doubled, what is the new force of attraction between the two objects?
Answer: If the distance is increased by a factor of 2, then distance squared will increase by a factor of 4. Thus, the inverse square law implies that the force will be "1/4" of the original 16 units. Therefore, the force of gravity becomes 4 units.
2. Suppose the distance in question 1 is tripled. What happens to the forces between the two objects?
Answer: Again using inverse square law, we get distance squared to go up by a factor of 9. The force decreases by a factor of 9 and becomes 1.78 units.
3. If you wanted to make a profit in buying gold by weight at one altitude and selling it at another altitude for the same price per weight, should you buy or sell at the higher altitude location? What kind of scale must you use for this work?
Answer: To profit, buy at a high altitude and sell at a low altitude. Explanation is left to the student.
Check Your Understanding
4. What would happen to your weight if the mass of the Earth somehow increased by 10%?
Answer: Your weight is nothing but force of gravity between the earth and you (as an object with a mass m). As shown in the above graph, changing one of the masses results in change in force of gravity. In this case, if the earth' mass goes up by 10%, then the force of gravity on you, or your weight, will increase by the same amount, that is 10%.
5. The planet Jupiter is more than 300 times as massive as Earth, so it might seem that a body on the surface of Jupiter would weigh 300 times as much as on Earth. But it so happens a body would scarcely weigh three times as much on the surface of Jupiter as it would on the surface of the Earth. Explain why this is so.
Answer: The effect of greater mass of Jupiter is partly off set by its larger radius which is about 10 times the radius of the earth. This means the object is times farther from the center of the Jupiter compared to the earth. Inverse of the distance brings a factor of 100 to the denominator and as a result, the force increases by a factor of 300 due to the mass, but decreases by a factor of 100 due to the distance squared. The net effect is that the force increases 3 times.
After reading this section, it is recommended to check the following movie of Kepler's laws.
http://www.archive.org/details/kepler_full_cc (movie length is about 7 minutes)
Newton's law of gravitation was preceded by three important discoveries about planetary motion by the German astronomer Johannes Kepler.
Kepler's three laws of planetary motion can be described as follows:
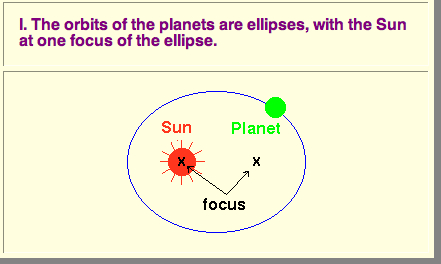
Kepler's First Law is illustrated in the image shown above. The Sun is not at the center of the ellipse, but is instead at one focus (generally there is nothing at the other focus of the ellipse). The planet then follows the ellipse in its orbit, which means that the Earth-Sun distance is constantly changing as the planet earth goes around its orbit. For purpose of illustration we have shown the orbit as rather eccentric; remember that the actual orbits are much less eccentric than this.
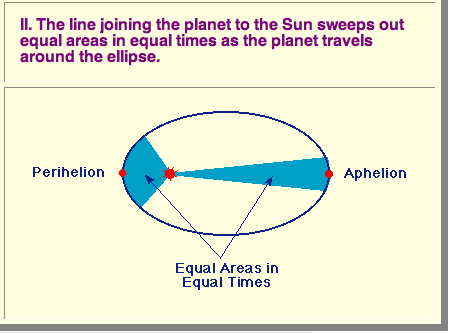
Kepler's second law is illustrated in the preceding figure. The line joining the Sun and planet sweeps out equal areas in equal times, so the planet moves faster when it is nearer the Sun. Thus, a planet executes elliptical motion with constantly changing angular speed as it moves about its orbit. The point of nearest approach of the planet to the Sun is termed perihelion; the point of greatest separation is termed aphelion. Hence, by Kepler's second law, the planet moves fastest when it is near perihelion and slowest when it is near aphelion.

In this equation P represents the period of revolution for a planet (in some other references the period is denoted as "T") and R represents the length of its semi-major axis. The subscripts "1" and "2" distinguish quantities for planet 1 and 2 respectively. The periods for the two planets are assumed to be in the same time units and the lengths of the semi-major axes for the two planets are assumed to be in the same distance units. Kepler's Third Law implies that the period for a planet to orbit the Sun increases rapidly with the radius of its orbit. Thus, we find that Mercury, the innermost planet, takes only 88 days to orbit the Sun but the outermost planet (Pluto) requires 248 years to do the same.
There is a popular misconception that the seasons on the Earth are caused by varying distances of the Earth from the Sun on its elliptical orbit. This is not correct. One way to see that this reasoning may be in error is to note that the seasons are out of phase in the Northern and Southern hemispheres: when it is Summer in the North it is Winter in the South.
The primary cause of the seasons is the 23.5 degree of the Earth's rotation axis with respect to the plane of the ecliptic, as illustrated in the adjacent image . This means that as the Earth goes around its orbit the Northern hemisphere is at various times oriented more toward and more away from the Sun, and likewise for the Southern hemisphere, as illustrated in the following figure.
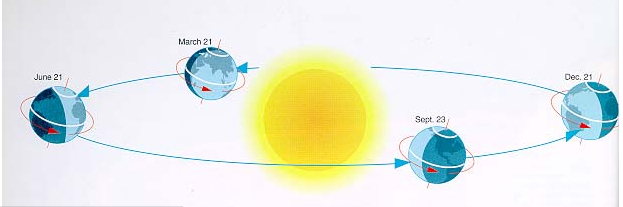
Thus, we experience Summer in the Northern Hemisphere when the Earth is on that part of its orbit where the N. Hemisphere is oriented more toward the Sun and therefore the Sun rises higher in the sky and is above the horizon longer, and the rays of the Sun strike the ground more directly. Likewise, in the N. Hemisphere Winter the hemisphere is oriented away from the Sun, the Sun only rises low in the sky, is above the horizon for a shorter period, and the rays of the Sun strike the ground more obliquely.
In fact, as the diagram indicates, the Earth is actually closer to the Sun in the N. Hemisphere Winter than in the Summer (as usual, we greatly exaggerate the eccentricity of the elliptical orbit in this diagram). The Earth is at its closest approach to the Sun (perihelion) on about January 4 of each year, which is the dead of the N. Hemisphere Winter.
On June 21, the summer solstice, the top of the axis (the North Pole) is
pointed directly toward the sun. Areas north of the equator experience longer
days and shorter nights.
On December 21, the winter solstice, the top of earth's axis is pointed directly
away from the sun. Areas north of the equator experience shorter days and longer
nights.
Halfway in between the summer and winter solstices are the equinoxes. At these
times the earth's axis is pointing neither toward nor away from the sun. On
both equinoxes, all locations on earth receive exactly 12 hours of daylight
and 12 hours of night.
As is clear from the preceding diagram, the seasons in the Southern Hemisphere are determined from the same reasoning, except that they are out of phase with the N. Hemisphere seasons because when the N. Hemisphere is oriented toward the Sun the S. Hemisphere is oriented away, and vice versa:
The tides at a given place in the Earth's oceans occur about an hour later each day. Since the Moon passes overhead about an hour later each day, it was long suspected that the Moon was associated with tides. Newton's Law of Gravitation provided a quantitative understanding of that association.
Consider a water molecule in the ocean. It is attracted gravitationally by the Earth, but it also experiences a much smaller gravitational attraction from the Moon (much smaller because the Moon is much further away and much less massive than the Earth). But this gravitational attraction of the Moon is not limited to the water molecules; in fact, the Moon exerts a gravitational force on every object on and in the Earth. Tides occur because the Earth is a body of finite extent and these forces are not uniform: some parts of the Earth are closer to the Moon than other parts, and since the gravitational force drops off as the inverse square distance, those parts experience a larger gravitational tug from the Moon than parts that are further away.
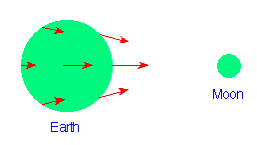 |
In this situation, which is illustrated schematically in the adjacent figure, we say that differential forces act on the body (the Earth in this example). The effect of differential forces on a body is to distort the body. The body of the Earth is rather rigid, so such distortion effects are small (but finite). However, the fluid in the Earth's oceans is much more easily deformed and this leads to significant tidal effects. |
We may illustrate the basic idea with a simple model of a planet completely covered by an ocean of uniform depth, with negligible friction between the ocean and the underlying planet, as illustrated in the adjacent figure. The gravitational attraction of the Moon produces two tidal bulges on opposite sides of the Earth.
| Without getting too much into the technical details, there are two bulges because of the differential gravitational forces. The liquid at point A is closer to the Moon and experiences a larger gravitational force than the Earth at point B or the ocean at point C. Because it experiences a larger attraction, it is pulled away from the Earth, toward the Moon, thus producing the bulge on the right side. Loosely, we may think of the bulge on the left side as arising because the Earth is pulled away from the water on that side because the gravitational force exerted by the Moon at point B is larger than that exerted at point C. Then, as our idealized Earth rotates under these bulges, a given point on the surface will experience two high and two low tides for each rotation of the planet. | 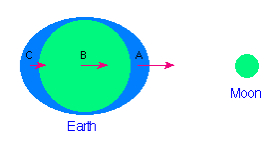 |
Another complication of a realistic model is that not only the Moon, but other objects in the Solar System, influence the Earth's tides. For most their tidal forces are negligible on Earth, but the differential gravitational force of the Sun does influence our tides to some degree (the effect of the Sun on Earth tides is less than half that of the Moon).
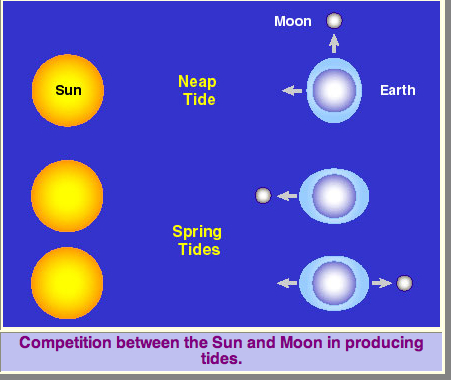
For example, particularly large tides are experienced in the Earth's oceans when the Sun and the Moon are lined up with the Earth at new and full phases of the Moon. These are called spring tides (the name is not associated with the season of Spring). The amount of enhancement in Earth's tides is about the same whether the Sun and Moon are lined up on opposite sides of the Earth (full Lunar phase) or on the same side (new Lunar phase). Conversely, when the Moon is at first quarter or last quarter phase (meaning that it is located at right angles to the Earth-Sun line), the Sun and Moon interfere with each other in producing tidal bulges and tides are generally weaker; these are called neap tides. The figure shown above illustrates spring and neap tides.
It is highly recommended that you check the following interesting simulation of the ocean tides.
https://beltoforion.de/en/tides/simulation.php#idStart