
Stars rising in the east, as viewed from Ogden, Utah. The camera was mounted on a tripod and the shutter was left open for ten minutes, to show the stars’ apparent motion. The foreground mountains were illuminated by city lights.
We begin with the stars. Even today, when we’re distracted by indoor living and artificial lights, most of us find the stars beautiful and fascinating. But imagine how they must have captivated our ancestors, who spent far more time under the starry night sky!
For thousands of years, people have wondered about the stars. What are they? How far away are they? What is the meaning of their arrangement in the sky? How do their locations in the sky change over time, and why?
This last question turns out to be the easiest to answer, so it’s a natural place to begin our study of astronomy. As you’ll see, the answer ends up telling us only a little about the stars, but a great deal about the earth.
Here’s a time-exposure photo that vividly illustrates the motion of the stars through a portion of our sky:

Stars rising in the east, as viewed from Ogden, Utah. The camera was mounted on a tripod and the shutter was left open for ten minutes, to show the stars’ apparent motion. The foreground mountains were illuminated by city lights.
As time passes, the stars rise in the east (just like the sun). But notice that they rise diagonally, not straight up. The diagonal goes from north (left) to south (right). After a few hours, these same stars will appear high in the southern sky.
Turning to face south, we see that the stars there are moving from left (east) to right (west):

Ten-minute time exposure facing south and slightly west, from the same location as the previous photo. The stars are moving from left (east) to right (west) across the field of view. Despite the annoying light pollution, you can barely make out part of the Milky Way, right of center.
By now you can probably guess that stars set in the western sky, again along a diagonal:

Ten-minute time exposure facing west, from the same location as the previous two photos. The stars are setting along a diagonal, from south (left) to north (right). The bright star at the lower-right is Arcturus.
And in the north, the motion is most interesting. Stars rise in the northeast and set in the northwest, moving in counter-clockwise circles around a point that's high above the northern horizon:

Half-hour time exposure facing north and slightly west, from the same location as the previous three photos. The stars are tracing counter-clockwise circles, centered on a point near the prominent North Star (Polaris). Notice the Big Dipper at the lower-left.
The magestic motions of the night sky were intimately familiar to ancient people. Today this familiarity has been lost (except by astronomy geeks), so you'll need to make a special effort to remember and visualize the patterns. It helps to stand under the night sky and point with your hands, tracing out the paths of different stars. In summary:
Besides direct observation, you can get accustomed to these motions by playing with the Sky Motion Applet that I've created for this purpose. A variety of other useful resources are listed at the bottom of this page.

Orion the Hunter is one of the brightest and most familiar constellations of the night sky. The row of three stars near the middle is called Orion's Belt.
Notice also that as the stars move through the sky, they stay in the same patterns. That is, the apparent “distance” between any two stars never changes. A given pattern of stars may move across the sky and turn sideways or even upside-down, but it won't grow larger or smaller, or change its shape in any other way.
The permanence of the stellar patterns encourages us to mentally connect the dots to make pictures, called constellations. Different cultures have done this in different ways, and you might enjoy making up your own constellations when you're out under the stars. To better communicate, however, professional astronomers have agreed on a set of 88 official constellations, many of which originated with the ancient Greeks. Some of the official constellations are easy to recognize, while others are obscure and difficult. Learning the constellations is helpful if you want to navigate or tell time by the stars, or determine where to look in the sky for a particular star or other interesting object.
If you want to learn the constellations, you can start with the Sky Motion Applet and then move on to some of the resources listed at the bottom of this page.
When we talk about the apparent "distance" between two points in the sky, we're really talking about an angle, measured between the two imaginary lines running from your your eye out to those points:
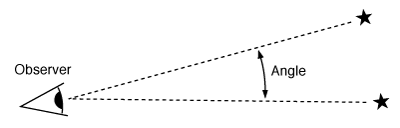
The angle between two points in the sky is defined as the angle between two imaginary lines running from you out to those points. For the two stars shown, the angle is about 16 degrees.
The bigger the angle, the farther apart the two points appear to be in the sky. The actual distance between two stars is much harder to determine, as we'll later see.
Here's a photo of the Big Dipper, with some of the angles between stars labeled:
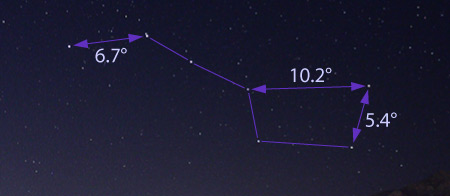
The bowl of the Big Dipper is about 10° wide and 5° deep. The entire handle is 16° long, and the whole Dipper is 26° long.
Similarly, the width of Orion's Belt is a little under 3°, and the four star-trail photos above each span a width of about 60° from side to side.
To measure the angles between stars and other points in the sky, astronomers use protractors and similar instruments, often attached to a telescope for accurate pointing. To get an approximate measurement, however, you can use instruments that are always with you: your hands. The width of your fist, held at arm's length, is about 10°, while the width of your little finger tip, also held at arm's length, is about 1°. These angles don't depend much on your size, because people with bigger hands also tend to have longer arms. Next time you see the Big Dipper, hold out your fist and check that the Dipper's bowl is about one fist wide. To estimate larger angles you can use both hands to count multiple fists. It's also helpful to remember that the angle between the horizon and zenith (straight overhead) is 90°, as is the angle between two adjacent cardinal directions such as north and east, or east and south.
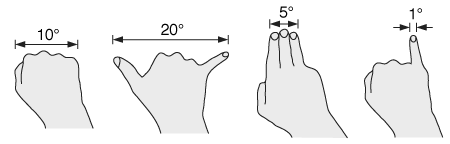
Angle estimates using fist and fingers, with arm outstretched.
Question: How many fists, stacked one on top of another, would it take to reach from the horizon to zenith?
Now look back at the east- and west-facing star trail photos at the top of this page. The stars in these photos are following circular arcs that begin in the east, pass high across the southern sky, and end in the west. You, the observer, are at the approximate center of these circular arcs, so you can directly measure the angle through which these stars move, by holding up your hands (to the real sky, not the photo!). If you make this measurement carefully, you'll find that in 10 minutes, each of these stars moves through an angle of 2.5°. The rate of motion is steady, so simple multiplication or division allows us to calculate the angle for any other time period: 5° in 20 minutes, 7.5° in 30 minutes, 15° in an hour. Over a full 24-hour day, the angle of rotation would be
The stars therefore complete a full circle (360°) in 24 hours. (Of course, you normally can't see the stars during daylight, but they're still there and still following their circular paths, as you can confirm with a telescope or by getting above earth's atmosphere.)
Question: How many minutes would it take for a star to move just one degree? (Calculate the answer carefully—don't just guess.)
The rate of angular motion is the same in other parts of the sky, although you can't just measure the angles with your hands because you're not at the center of the circles. In the northern sky, however, you can measure the angles directly by laying a protractor down on a photograph. Here's a longer time exposure of star trails near the North Star:

In the northern sky, all stars move at the same rate around the common center of their circles. During this 75-minute time exposure, the stars rotated by approximately 19°.
If you use the information in this photo to calculate the time for a one-degree rotation (or 15° or any other angle), you should get approximately the same answer as above.
Question: How would you use the data from the preceding photo to calculate the time required for a one-degree rotation?

This computer-simulated multiple-exposure image (made with Sky Motion Applet) shows Orion in the southern sky at the same time on seven successive nights. Each night, after completing a full circle, the stars have shifted rightward by about one degree.
To be precise, though, I need to tell you that all of the angles quoted above are only approximate. In fact, it takes a little less than an hour for the stars to move by 15°, and therefore it takes a little less than 24 hours for the stars to complete an entire circle. In fact, it takes just 23 hours and 56 minutes, or four minutes less than a full day. During those last four minutes the stars will move by an additional degree, so in exactly 24 hours, the stars actually move by 361°, not 360.
These extra 1° rotations add up over the weeks and months, so that after a full year, at any given time of night, you'll see the stars in the same positions as before. (Since a year is 365 days, not 360, you can probably guess that the extra per-day rotation is actually slightly less than 1°. If you really want to be precise about these things, you also need to take into account leap years—but let's not bother.)
So, as the seasons pass, we see different groups of stars in a given direction, at any given time of night. In January you can watch Orion rising in the east just after sunset, but by March, Orion will be high in the south, heading westward, by the time the sky is dark. Meanwhile the bright star Arcturus will be rising in the east, a sign that spring is coming. If you learn to identify the prominent stars and constellations, they will give you a strong sense of the passage of the seasons. Night owls and early risers can also enjoy a preview of the stars that evening observers will see in the coming months.
To simplify their understanding of the motions of the sky, ancient people invented a mechanical model to explain these motions. We still use this model today because it's so convenient—even though it's wrong. If you can visualize the model, you won't have to memorize a whole bunch of separate facts about how the stars move.
The stars appear to be attached to a giant celestial sphere, spinning about the celestial poles, and around us, once every 23 hours and 56 minutes.
The model is simply that the stars are all attached to the inside of a giant rigid celestial sphere that surrounds the earth and spins around us once every 23 hours, 56 minutes. The spinning carries each star around in its observed circular path, while a special point in the northern sky, at the center of the circles, remains fixed. The sphere's rigidity accounts for how the shapes of the constellations never change, and its enormous size accounts for how the constellations never grow or shrink, as they would if a particular point on earth were significantly closer to one side of the sphere than the other.
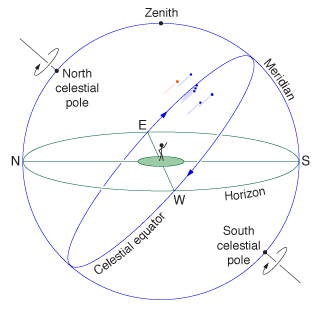
To better describe locations in the sky, we give names to the various parts of the celestial sphere. The fixed point in the northern sky is called the north celestial pole, and is located only about a degree away from the famous North Star (which makes tiny circles around it). Ninety degrees from the pole is the celestial equator, a great circle that runs from directly east to directly west, passing high above our southern horizon. Mintaka, the rightmost star in Orion's Belt, happens to lie almost exactly on the celestial equator, so you can think of the celestial equator as tracing the path of this star. Another important great circle is the meridian, which runs from directly north to directly south, passing straight overhead. As the sphere turns, the meridian remains fixed in the sky. The point straight overhead is called zenith.
I've described the stellar motions as they appear from my home in Ogden, Utah, at a latitude of 41° north of the equator. What about other locations?
Moving east or west makes no difference, except to determine when you see things. If you live farther east, you'll see any given star rise and set sooner; if you live farther west, each star rises and sets later. We compensate for these differences, in an approximate way, by setting our clocks according to different time zones.
Moving north or south is more interesting. The farther north you go, the higher in the sky you'll see the north celestial pole and the stars around it—and the lower all the stars will appear in the south. In fact, the angle between your northern horizon and the north celestial pole is precisely equal to your latitude.
For example, in Ogden the north celestial pole is 41° above my northern horizon, but if you're in Anchorage, Alaska, the angle is 61°. At the earth's north pole, you would see the north celestial pole straight overhead, and the celestial equator would lie along your horizon, so you would never see any stars rise or set; they would just move in counter-clockwise circles if you're facing upward, or horizontally to the right if you're facing the horizon. Stars below your horizon (that is, south of the celestial equator) would always be hidden from your view.
On the other hand, if you travel south to Mexico City, you'll see the north celestial pole only 19° above your northern horizon. The Big Dipper will no longer always be visible, setting in the northwest and rising in the northeast instead. But in the southern sky, you'll see stars that are never visible in Utah, including the famous Southern Cross.
Farther south, at earth's equator, the north celestial pole lies on the northern horizon, and the celestial equator passes straight overhead. From here, as the constellations rise in the east, they appear to head straight up, rather than along a diagonal. In the west, they head straight down as they set. Even more stars are visible in the southern sky, making clockwise half-circles about a point on the southern horizon, the south celestial pole.
From the southern hemisphere, you can't see the north celestial pole at all. The south celestial pole, however, will appear above your southern horizon, by an angle equal to your southern latitude. Stars rising in the east will head upward and to the left, toward the northern sky. The celestial equator will also pass through the northern sky, lower and lower as you head farther south.

This several-hour-long time exposure, taken from tropical northern Australia, shows the clockwise motion of the southern stars around the south celestial pole. The trails of the Southern Cross start at the top of the image, with the top of the cross initially above the edge. Photo by David Miller/DMI.

The ancient Greeks conceived the universe as a giant sphere of stars, surrounding the much smaller spherical earth. In this modern plastic model, however, the size of the earth is greatly exaggerated in comparison to the celestial sphere.
Finally, if you visit earth's south pole, you'll see the south celestial pole straight overhead, with the stars making clockwise circles around it. The celestial equator will lie on your horizon, with the stars moving parallel to it, from right to left. You always see the same half of the celestial sphere, completely distinct from the half that you would see from earth's north pole.
The explanation for all these effects is simply that the earth's surface is curved. So when you travel to a different location, your horizon tilts with respect to the stars. Today every school child is taught that the earth is (approximately) a sphere. Even in ancient times, however, astute travelers realized that the changes in the stars as you travel north or south must be caused by the curvature of the earth. The ancient Greeks even reasoned that the earth must be a sphere, and thus pictured the universe as a pair of spheres: an enormous celestial sphere, carrying the stars around us once a day, and the much smaller spherical earth, fixed at the center of the universe.

The photo at right shows Orion near the western horizon. The photo was not taken from Utah.
Question 1: Is Orion rising or setting?
Question 2: From what latitude was this photo taken?
Question 3: About how long was the camera shutter open?
Once you understand how the earth's curvature makes the stars shift as you travel, you can easily determine the earth's circumference. All you have to do is travel directly north or south for some measured distance, and measure the angular shift of stars near the meridian. Since the North Star is always very close to the meridian (and easy to learn to recognize), it's probably the most convenient reference star.
The only real difficulty with this measurement is that you have to travel pretty far before the shift becomes noticeable. If you're careful, though, you can measure an angular shift of one degree whenever you travel directly north or south by about 70 miles. So, for instance, if you travel from Ogden to Provo (70 miles south), you'll see the North Star get lower in the sky by 1°. By the same token, stars in the southern sky will get higher by 1°. (Of course, it's hard to measure a shift of only 1°, so it's best to travel farther than 70 miles and measure the proportionally larger angles.)
Now imagine continuing your journey southward. For every 70 miles traveled, the stars shift by 1°. After 700 miles, the stars would shift by 10°. As you cross the equator, the North Star would disappear below your horizon, but you could continue to measure the shifts in the new stars that you see in the south. Eventually you would come to the south pole, then continue past it, now traveling northward, back to the equator, then to the north pole, and finally around to your starting point. The stars have now shifted by a full 360-degree circle, back to their original positions. And to accomplish this, you would have to travel a total distance of approximately
The earth's circumference is therefore about 25,000 miles. The circumference around the equator is also about 25,000 miles, though this is a little harder to measure. You may find it easy to remember that at the equator, each of the 24 (idealized) time zones is about 1000 miles wide.
Question: Did you check my calculation of the earth's circumference? If not, check it now! Which statement best describes my accuracy?
Exercise: Use this value of the circumference to calculate the diameter of the earth in miles, rounded to the nearest thousand.
The first person known to have done this calculation was the ancient Greek astronomer Eratosthenes. Instead of using the North Star for reference he used the noon sun, which is also on the meridian. There's some dispute over how accurate his calculations actually were, but the important thing is that he used a valid method to calculate earth's size, more than 2100 years ago. (If you were taught as a child that everyone before Columbus thought the earth was flat, you were lied to. Columbus was ridiculed not for believing the earth to be a sphere, but for grossly underestimating its size, thinking he could sail all the way to Asia before running out of provisions. He was extremely fortunate to hit land long before he would have reached east Asia.)
Throughout this discussion I've described the motions of the stars with respect to our horizon. It's natural to assume that our horizon, and hence the earth below it, is truly fixed, and therefore that the stars truly move around in huge circles once each day.
But if you think about it, we can account for all the same observations if we assume that the stars are fixed in space, and the earth spins around once each day (in the opposite direction). The first person known to have suggested this possibility was another ancient Greek, Heraclides. But the idea didn't catch on for another 1900 years, because it seemed so obvious to everyone that the earth doesn't move. (After all, just look at it! Does the earth look like it's moving? So there!)
Today, of course, we know that Heraclides was right. It really is the earth that spins in circles, not the stars. I'll explain later how we know this, and how it's possible for the earth to spin at tremendous speed without our feeling it. Meanwhile, you have my permission to say that the stars "rise" and "set" and "move" through the sky—as long as you keep "with respect to our horizon" in the back of your mind.
There are tons of great resources out there that can help you learn about stellar motions, constellations, and the celestial sphere:
Copyright ©2010-2011 Daniel V. Schroeder. Some rights reserved.