The apparent positions and separations of objects in the sky are not determined by the linear distances between two objects but by their angular separation. For example, the angular distance from the horizon to directly overhead, the zenith, is 90°. Not only can we measure the angular separation between two objects, but we can also measure the angular size of an object such as the Moon, which is about 0.5°.
How many Moons could you line up, side by side, to extend from the horizon to the zenith? What do you think is the angular size of the Sun?
Since the Moon or the Sun isn't always available to use as a basis to measure angular sizes, here are a few handy rules (of thumb!) that you should remember. With your arm outstretched, one fingerwidth is ~2°, one fistwidth ~10°, and one handspan ~20°. This technique works because an angle depends on the ratio of (a) the linear size d (cm) of the object to (b) the distance D (cm) to the object. Since the ratio of finger size to arm size is approximately the same for different persons, most people have a fingerwidth of ~2° no matter what the length of their arms. But it is still best if you calibrate your own body using the moon and objects that you have measured with your cross staff.
When you start to measure angular sizes, you will soon realize that there is a relation between the angular size of an object and the distance to that object. In the classroom, your TA will instruct you to measure the angular size of a globe from different distances in the room. How do you expect the angular size a will vary with your distance D from the globe? The appropriate formula is
a = 57.3° (d / D)
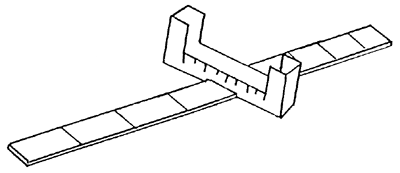
The cross staff is a simple device (used for centuries before ~ AD 1600) for measuring the angular separation between two objects, or the angular size of a single object and (sometimes) thereby deriving its linear size or distance. It consists of a yardstick and a crosspiece attached at a right angle. All you have to do is sight an object along the stick and slide the crosspiece back and forth (or change your own distance from the object) until the apparent or angular size of the crosspiece (or some portion of it) matches the apparent or angular size of the distant object.

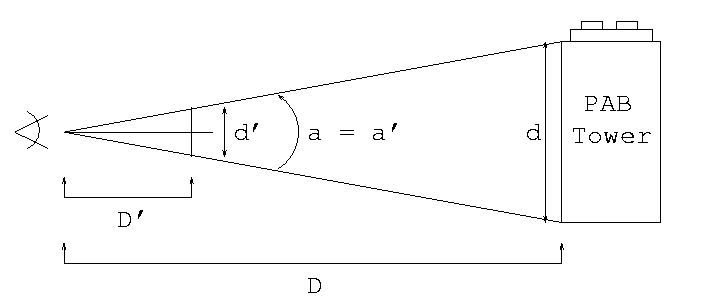
Note that the angle from the top to the bottom of the crosspiece is the same as the angular size of the building. If D' is the "working" length of the cross staff and d' the width of the crosspiece, then the angular size of the crosspiece is a' = 57.3° (d' / D') . But this value of a' is also the angular size of the building. Thus if you measure the distance D to the building, you can derive its height d. Measure the distance to the building by pacing it off. Of course you must also determine the length of your step -- another good use for your yardstick! (You should determine your step's length over at least a 30-foot course.)
Measure the height of the tower of the Physics/Astronomy Building from the plaza level. See the sketch to know exactly what we define as the "top" of the tower. Later, on your own, measure the height from the pavement of the prominent sculpture in Red Square ("Broken Obelisk" by Barnett Newman). If it is clear before the assignment is due, measure the angular separations between a few different bright stars that you identify using your Sky Chart, or measure the size of a couple of prominent constellations such as the Big Dipper. Turn in all your measurements and calculations.
To construct your cross-staff, follow the instructions below carefully. You will need good (sharp and pointy!) scissors, glue, and your yardstick.