SKYWATCH PROJECT: DETERMINING THE EARTH'S CIRCUMFERENCE

EQUIPMENT REQUIRED FOR SUN OPTION: A stick at least one foot long which can be driven into the ground (or a "plumber's helper" works great!), a measuring device (tape measure or ruler), a watch, a string with a weight tied to its end, a car, and gasoline.

EQUIPMENT REQUIRED FOR POLARIS OPTION: Homemade quadrant, as used for the first Skywatch, plus car and gasoline.

TIME REQUIRED: Two days when you can make (a) observations of the sun's altitude between 11:15 a.m. and 12:45p.m. PST (equivalent to 12:15 p.m. to 1:45 p.m. PDT) or (b) observations of Polaris's altitude. One of these days should be in Seattle and the other day at least 150 miles north or south of Seattle, say in Portland or Vancouver, B.C. You need not go exactly due north or south, but the experimental results are simpler to interpret if you don't wander too far east or west. Basically you need to go into Canada or south of the state -- Boise or San Francisco are O.K., but Spokane or Walla Walla are not. If necessary, the observations can be made several days apart (or even weeks apart), but then a correction for the sun's changing position needs to be made. Even for observations on consecutive days, your answer will be more accurate if you allow for this -- use the table of solar declinations given in the "Celestial Navigation" handout.

BACKGROUND: Eratosthenes (ca. 276-192 B.C.) was a Greek scholar in the Egyptian city of Alexandria, the great center of learning of the Mediterranean world in the days of the ascendancy of the Roman Empire. He is credited with having applied simple geometric reasoning to obtain an excellent estimate of the earth's circumference. His derived value appears to have been within 10% of today's accepted value, but more importantly his reasoning was clear and correct. The accuracy of his estimate was limited only by the precision of the instruments he used, as well as his value for the distance between Alexandria and Syene (present day Aswan). Eratosthenes's method can also be used by you today.

PROCEDURE USING THE SUN: At each site drive a stick into a level, smooth (ideally no grass) piece of ground, making it as close to vertical as possible (holding a string and weight can provide a reference). A "plumber's helper" can also serve for your gnomon. Beginning about 12:15 p.m. PDT (or 11:15 a.m. PST) carefully measure and record the length of the stick's shadow every 10 minutes. Continue this until you are certain that you have observed the shadow at its shortest. Before you remove the stick from the ground, carefully measure the length of that part of the stick above ground. This procedure should be exactly repeated at each site.

PROCEDURE USING POLARIS: Use your quadrant to determine the latitude at each site using Polaris. The advantage with Polaris is that the observations are not complicated by doing them on separate days, although they still should be carried out at the same time of night, since Polaris is not exactly at the north celestial pole. If you do observe at different times of the night, use the method in the "Celestial Navigation" handout to find the required correction.

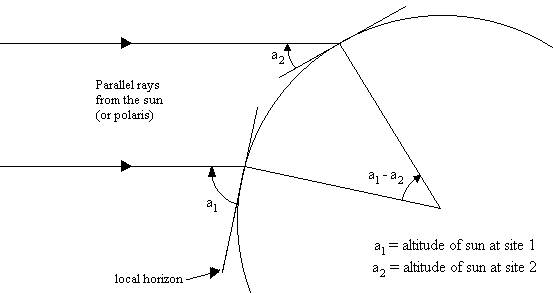
CALCULATIONS: The attached sketch lays out the geometry that Eratosthenes used for his determination of the Earth's circumference. Apply simple trigonometry to convert your measurements of the shadow's length to the altitude a of the sun at local noon at your two observation points. Simple geometrical considerations will show you that the ratio of the north-south distance d to the entire circumference of the earth C is equal to the ratio of the angle (a₁ -a₂ ) (which you have measured) to a full circle of 360 degrees. In other words:

d a₁ – a₂

¾ = ¾¾¾

c 360^O

If your two sites are close to being north-south and the road is reasonably straight, then you can find d from your car's odometer. In other cases, and for greater accuracy in all cases, d should be measured on a map as the north-south component of the separation between the sites. For example:

You can now solve for the circumference of the earth and consider yourself a geodesist. You naturally will want to compare your result with the accepted value, as well as check your measured value of (a₁ -a₂) with the difference in the latitudes of the two sites. The Times Atlas of the World, available at Suzzallo Library Reference, is one good source of latitudes for towns.