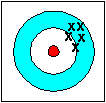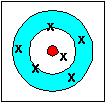
There are two kinds of numbers in the world:

• exact:
  • example: There are exactly 12 eggs in a dozen.
• inexact numbers:
  • example: any measurement.
    If I quickly measure the width of a piece of notebook paper, I might get 220 mm (2 significant figures). If I am more precise, I might get 216 mm (3 significant figures). An even more precise measurement would be 215.6 mm (4 significant figures).

Accuracy refers to how closely a measured value agrees with the correct value.
Precision refers to how closely individual measurements agree with each other.

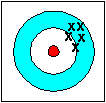accurate (the average is accurate) not precise	precise not accurate	accurate and precise

A rule of thumb: read a measurement to 1/10 or 0.1 of the smallest division. This means that the error in reading (called the reading error) is 1/10 or 0.1 of the smallest division on the ruler or other instrument. If you are less sure of yourself, you can read to 1/5 or 0.2 of the smallest division.

Rules for Significant Figures:

1. Leading zeros are never significant.
   Imbedded zeros are always significant.
   Trailing zeros are significant only if the decimal point is specified.
   Hint: Change the number to scientific notation. It is easier to see.

2. Addition or Subtraction:
   The last digit retained is set by the first doubtful digit.

3. Multiplication or Division:
   The answer contains no more significant figures than the least accurately known number.

EXAMPLES:

	Example	Number of Significant Figures	Scientific Notation
	0.00682	3	6.82 x 10 -3	Leading zeros are not significant.
	1.072	4	1.072 (x 10 0)	Imbedded zeros are always significant.
	300	1	3 x 102	Trailing zeroes are significant only if the decimal point is specified.
	300.	3	3.00 x 102
	300.0	4	3.000 x 102

EXAMPLES

Addition		Even though your calculator gives you the answer 8.0372, you must round off to 8.04. Your answer must only contain 1 doubtful number. Note that the doubtful digits are underlined.
Subtraction		Subtraction is interesting when concerned with significant figures. Even though both numbers involved in the subtraction have 5 significant figures, the answer only has 3 significant figures when rounded correctly. Remember, the answer must only have 1 doubtful digit.
Multiplication		The answer must be rounded off to 2 significant figures, since 1.6 only has 2 significant figures.
Division		The answer must be rounded off to 3 significant figures, since 45.2 has only 3 significant figures.

Notes on Rounding

• When rounding off numbers to a certain number of significant figures, do so to the nearest value.
  • example: Round to 3 significant figures: 2.3467 x 10⁴ (Answer: 2.35 x 10⁴)
  • example: Round to 2 significant figures: 1.612 x 10³ (Answer: 1.6 x 10³)

• What happens if there is a 5? There is an arbitrary rule:
  • If the number before the 5 is odd, round up.
  • If the number before the 5 is even, let it be.
    The justification for this is that in the course of a series of many calculations, any rounding errors will be averaged out.

  • example: Round to 2 significant figures: 2.35 x 10² (Answer: 2.4 x 10²)
  • example: Round to 2 significant figures: 2.45 x 10² (Answer: 2.4 x 10²)

  • Of course, if we round to 2 significant figures: 2.451 x 10², the answer is definitely 2.5 x 10² since 2.451 x 10² is closer to 2.5 x 10² than 2.4 x 10².