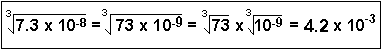
| 1,000,000,000,000,000,000,000,000,000,000 = 1 x 1030 | We don't even have a word for this. It's the mass of the Sun in kilograms. |
| 100,000,000,000,000,000,000,000 = 1 x 1023 | One hundred trillion billion: The approximate number of stars in the Universe |
| 40,100,000,000,000 = 4.01 x 1013 | 40.1 Trillion: the distance (in km) to the nearest star, Proxima Centauri. |
| 1,600,000,000,000 = 5.7 x 1012 | 5.7 Trillion: the number of dollars in the U.S. national debt, circa 2000. |
| 200,000,000,000 = 2 x 1011 | Two Hundred Billion: Approximate number of stars in the Milky Way Galaxy. |
| 15,000,000,000 = 1.5 x 1010 | 15 Billion: Approximate age of the Universe (in years). |
| 6,000,000,000 = 6 x 109 | Six Billion: Approximate number of people on the planet, circa 2000. |
| 1,000,000,000 = 1 x 109 | One Billion: The number of Earth-sized planets that would fit into the Sun; Also the speed of light in km/hr |
| 100,000,000 = 1 x 108 | One hundred million: the radius of the Sun in meters. |
| 78,300,000 = 78.3 x 106 | 78.3 million: the minimum distance from the Earth to Mars. |
| 384,400 = 3.844 x 105 | Three hundred eighty four thousand, four hundred: the distance to the moon from Earth (in km) |
| 40,000 = 4 x 104 | Forty thousand: the distance around the Earth at the equator (in km). |
| 4,000 = 4 x 103 | Four thousand: The circumference of Pluto (in km). |
As you can see, the exponent of 10 is the number of places the decimal point must be shifted to give the number in long form. A positive exponent shows that the decimal point is shifted that number of places to the right. A negative exponent shows that the decimal point is shifted that number of places to the left. (None of these appear above, because they would be really SMALL numbers...but you get the idea!)
The number of digits reported indicates the number of significant figures. This can help you figure out when the zeroes are important, and when they are just "place-holders".
How to do calculations:
On your scientific calculator:
Make sure that the number in scientific notation is put into your
calculator correctly.
Read the directions for your particular calculator. For
most scientific calculators:
To check yourself, multiply 5 x 1010 by 6 x 10-4 on your calculator. Your answer should be 3 x 107 (your calculator may say"3E7", which is the same thing).
If you don't have a scientific calculator, you will need to know the following rules for combining numbers expressed in scientific notation:
Addition and Subtraction:
Division:
Powers of Exponentials:
Roots of Exponentials:
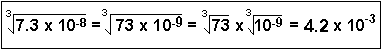
QUIZ:
| Question 1 | Write in scientific notation: 0.000467 and 32000000 |
| Question 2 | Express 5.43 x 10-3 as a number. |
| Question 3 | (4.5 x 10-14) x (5.2 x 103) = ? |
| Question 4 | (6.1 x 105)/(1.2 x 10-3) = ? |
| Question 5 | (3.74 x 10-3)4 = ? |
| Question 6 | The fifth root of 7.20 x 1022 = ? |
