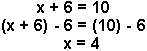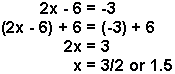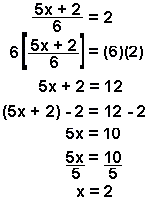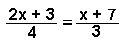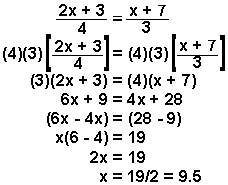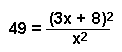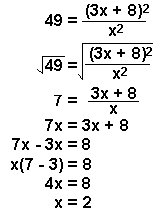The key to solving simple algebraic equations containing a single unknown (e.g. x + 6 = 10) is to realize that the equation is an equality. As long as you do the same mathematical operation (e.g. add a constant, subtract a constant, multiply by a constant, and divide by a constant) to both sides of the equation, the equality is still an equality. This includes squaring both sides of the equation or taking the square root of both sides of the equation.

Fundamental Laws:

• Distributive Law: 3(x + 2) = 3x + (3)(2) = 3x + 6
• Associative Law: 4x - 7x = x(4 - 7) = -3x

Example 1:	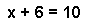To solve for x, subtract 6 from both sides of the equation
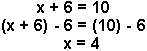Example 2:	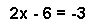To solve for x, add 6 to both sides of the equation divide both sides by 2.
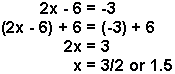
Example 3:	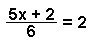To solve for x, multiply both sides by 6, subtract 2 from both sides, divide both sides by 5.
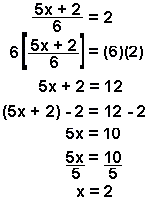Example 4:	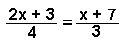To solve for x, multiply both sides of the equation by 4 and 3 to cancel out the denominators use the distributive law, by adding and subtracting, move the x terms to one side, and the non-x terms to the other side in line 5, use the associative law to simplify to get line 7, divide both sides by 2.
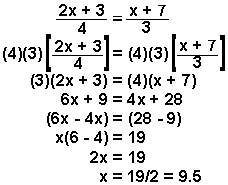Example 5:	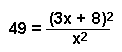This problem could be very complicated and become a quadratic equation. However, if you take the square root of both sides you are left in line 3 with a straightforward algebra problem.

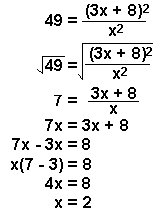QUIZ: Solve for x.

Question 1	Question 2	Question 3	Question 4