Materials
Meterstick

1. Let's see how the parallax of an object varies with distance.

   1. One partner takes the meterstick and places the pencil vertically at the 50 cm mark. The other partner places the "zero" end of the meterstick against her/his chin, holding it out horizontally. This partner then alternates opening and closing each eye, noting how the pencil moves against specific background objects.
   2. Have your partner move the pen half of the original distance (to 25 cm). When you alternate opening and closing each eye does the pen appear to move more or less than before? Try to quantify how much more or less (twice as much? one-third as much? etc.).
   3. Now, have your lab partner move the pen twice the original distance to you, to approximately the end of the meterstick. When you alternate opening and closing each eye does the pen appear to move more or less than before? Try to quantify how much more or less (twice as much? one-third times as much? etc.).

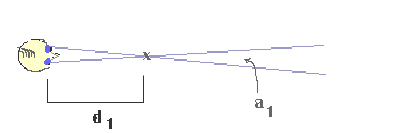
2. Here is a look at the approximate relationship between distance and parallax from a different viewpoint, from above the observer.

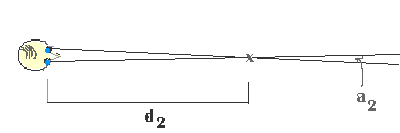   • The distance d₂ is twice the distance d₁. Does it qualitatively appear that angle a₂ is one-half of a₁?

   • When the distance is large enough that the parallax angle is very small, the parallax angle is proportional to the inverse of the distance (1/d). Conversely, if we can measure the parallax angle, we know that the distance to the object is proportional to the inverse of that angle.

   
   

3. There is a limit at which parallax becomes ineffective. This occurs when the parallax angle is so small that you can't see a change from one eye to the other. This distance is effectively infinity. You and your partner can find your personal infinity by taking the pencil farther and farther away from the observer until the parallax becomes undetectable.

   1. One of you should take the role of "observer" while the other walks straight away, holding the pencil out at arm's length, stopping every meter or so. The observer should alternate opening and closing each eye as the partner stops. How far away are you from each other when the pencil stops moving relative to even more distant objects?

   2. What can you determine about the usefulness of parallax at different distances?

4. To measure a parallax, you use a baseline: the distance between observation points. In the exercise above, the "baseline" is equal to the distance between the center of your eyes. Measure this distance for you and your partner. Compare these two numbers to the distances found in Step 3a. Is there a relationship between the two sets of numbers?
5. In astronomy, we use a "baseline" of the diameter of the Earth's orbit. The infinite background is made of stars much farther away than the star or object in question. We can measure accurate parallaxes of thousands of stars; unfortunately, most stars are simply too far to get an accurate parallax, and we must resort to other methods to determine their distances. Label the following on the image on the worksheet: Reference star(s), target star, Earth, Sun, dates of observation (choose one, then find the other consistent with that choice).
6. Technology improves all the time, and our options for choosing a baseline may be expected to expand. Which of the following scenarios would give the longest baseline for measuring parallax (and therefore would be most desirable)? Which is most feasible to do today? Why?
   1. A satellite orbiting high above the Earth.
   2. A telescope on the Moon.
   3. A satellite in Jupiter's orbit.
   4. A satellite in Pluto's orbit.