Distances to Stars in Leo

Summary
The student determines the distances to seven of the brightest stars in the constellation Leo using the method of spectroscopic parallax and compares the results to the more accurate distances derived from measured trigonometric parallaxes.

Background and Theory
If the distance to the star is known via its measured parallax, it is a trivial matter for astronomers, or anyone else for that matter, to determine the absolute magnitude of the star using the distance-magnitude relation. However, most stars are too far away to have a measurable parallax. In these cases, the distance to the star must be determined by some other method.
We can use our knowledge of the H-R Diagram and our analysis of a star's spectrum to determine stellar distances. From the strength of the lines in a star's spectrum, we can give it a spectral type and luminosity class. We can use the luminosity to find its absolute magnitude and thus its distance. Finding the distances to stars based upon their spectral type and luminosity is known as spectroscopic parallax (even though no parallax determination is involved). This method is neither easy nor exact; however, it has proved to be one of the best ways to learn about the more distant stars.
The first part of this method involves determining the star's spectral type and luminosity class. Astronomers can determine a star's spectral type based on the absorption lines in the spectrum of the star. The hottest stars show strong hydrogen lines and some helium lines. Spectral type A stars have predominately only hydrogen lines. As stars get cooler, more lines will appear as heavier elements [for example, calcium (Ca), and iron (Fe)] recapture their electrons. The singly ionized calcium atoms (Ca II) are especially strong in spectral type G stars. Spectral type K stars have very weak hydrogen lines but strong iron lines and similar heavy elements. The width of a line can be used to determine an approximate luminosity for a star. For a given element, supergiant stars will have narrow lines and dwarf stars will have broad lines. Here is an example of the luminosity effect for spectral type A0 stars, from A0 Ia to A0 V, and a white dwarf. Note that the lines of the white dwarf are so broad that they are smeared out.

Procedure
Print out the worksheet.

Table 1 on the worksheet lists the 14 stars Leo in order of their apparent magnitude. Seven of the stars have already been classified, and their absolute magnitudes and distances calculated. Your mission is to fill in the details for the other seven stars.

Figures 1 and 2 show a series of standard spectra used to classify stars (Fig. 1) and the seven stars in Leo that have already been classified as well as the seven that you need to classify (Fig. 2).
- First, take a look at the 7 stars in Leo that have already been classified, and compare each to the corresponding standard spectrum.
- Use the examples shown in Fig. 1 to guide you in classifying the remaining seven stars, shown in Fig. 2.
  Note: because of the need to keep the image sizes small, some image quality had to be sacrificed. Note, too, that there is a shift in some of the spectra. Let the line patterns and strengths guide you in your classification. Also, the standard spectra are for luminosity class V only. Do not worry about being extremely accurate -- this is not an exact science!
Enter your best guesses of the spectral types in column 3 of Table 1. The luminosity classes are already given.
Assign each star an absolute magnitude based on its spectral type and luminosity class. You must use the H-R Diagram to do this; find an HR Diagram having absolute magnitude vs. spectral type to use. Fill in column 6 of Table 1.
Solving for the distance in the distance-magnitude relation, M = m - 5 log (d) + 5, we get:
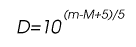Solve for the exponent of 10 first, then use either the inv log; keys or the 10^x key on your calculator.
Calculate the distance to each of the seven stars based upon the absolute magnitude from spectroscopic parallax.
For the seven unclassified stars, fill in Table 1 for the distances determined from the parallax values, where d = 1/parallax (d is in parsecs for parallax measured in seconds of arc).