
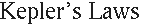
Summary
The student reviews Kepler's three laws, determines the properties of an ellipse and relates these properties to the orbits of planets and to binary stars.
Exercise
- Refer to your lecture notes and clearly label the parts (focus, semi-major axis, semi-minor axis, center) on the
following diagram of an ellipse:
- The eccentricity of an ellipse is defined as the distance from a focus to
the center of the ellipse divided
by the length of the semi-major axis. Calculate the eccentricity
of this ellipse: ___________
- State Kepler's First Law in your own words:
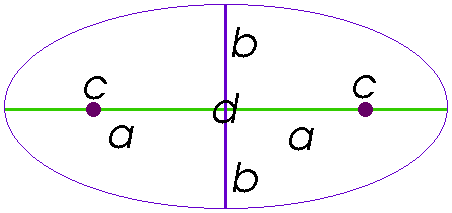
- Examine the figure of a planet; orbiting the Sun and fill in the blanks with the correct letter:
- Focus ____
- Aphelion ____
- Perihelion ____
- Increasing speed: ____ to ____
- Decreasing speed: ____ to ____
- Planet has greatest speed ____
- Planet has lowest speed ______
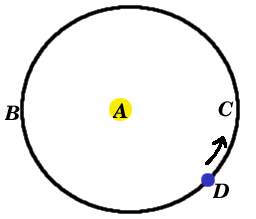
- Calculate the approximate eccentricities for the following ellipses:
- e =
- e =
- e =
- State Kepler's Second Law in your own words:
- Kepler's Third Law relates the _____________ (P) it takes a planet to go around the Sun in
an orbit of a given _________________________ (a).
Assume that the mass of the Sun is much, much greater than any
planet (which it is), and you measure P in years and
a in astronomical units.
The simplified relationship (formula) is: _________________
- The following two orbits have about the same value for a.
How do their values of P
compare? Explain your answer.

Kepler's Laws, so carefully derived from empirical work, were later
generalized to all celestial objects by Newton. For stars, we can not
assume that one object's mass is much greater than the other.
We can then use the full formula for Newton's generalization of Kepler's Third
Law.
- Write the full formula here: __________________________
- What relationship for the masses of the two stars can be derived from this formula?
- Ratio
- Difference
- Sum
- Product
- In general, we do not know the orbital inclination for the binary
(unless it is an eclipsing system). But we can still get some useful
information for the binary, since we know:
M1a1=M2a2
- What relationship for the masses of the two stars can be derived from this formula?
- Ratio
- Difference
- Sum
- Product
|
| We now have two equations and two unknowns (we determined
a if we know the distance to the stars) and can solve for the
mass of each star. |
(Optional)
Follow the steps given below for drawing ellipses on
this sheet.
Fill in the following table with your results.
| Ellipse | Major Axis |
Distance from
foci to center |
Eccentricity |
| 1 | | | |
| 2 | | | |
| 2 | | | |
Needed: 2 tacks (or thick straight pins), cardboard, about 15 cm length
of string, pencil
- Tack the sheet to a sized piece of thick cardboard, placing the tacks through the points marked "1".
- Tie the ends of the string together and loop it
around the tacks.
- Using the string as a guide (i.e., place the pencil inside the string loop and pull the loop taut), draw an ellipse.
- Repeat steps 1 and 2 with the tacks through points marked "2" (one tack
through the "top" 2, the other through the "bottom" 2. Finally, use just one tack through point "3."
(Figure out whether or not you will need to change the length of the string to keep the ellipse on the sheet of paper and adjust your methods accordingly!)
- Measure the major axis of each ellipse. Measure the distance between the
foci. Record these numbers in the above table.
- Calculate the eccentricity of each ellipse. Record the eccentricities in the table.
© 2003 Weber State University
Revised: 24 April, 2003




