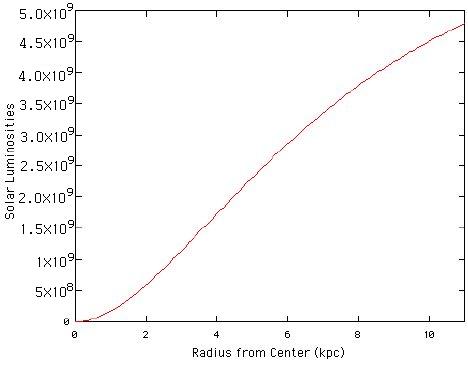
where G = 4.31 x 10-6
Use your values for Radius and Velocity to determine the mass interior to each radius. Record your results in the “Gravitational Mass” column in Table 1. Your numbers should be big. This is a galaxy, after all. It contains a lot of stars.
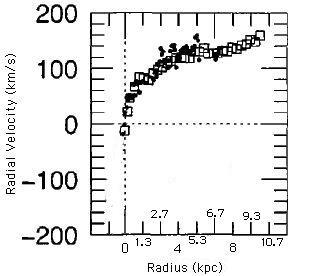 Procedure
Procedure