How many cycles did the star go through during the 14 days of observations?
- the orbit of the planet is circular (e = 0)
- the mass of the star is 1 solar mass
- the mass of the planet is much, much less that of the star
- we are viewing the system nearly edge on
- we express everything in terms of the mass and period of Jupiter
We make these assumptions to simplify the equations we have to use for determining the mass of the planet. The equation we must use is:
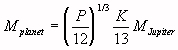
P should be expressed in years (or fraction of a year), and K in m/s. Twelve years is the approximate orbital period for Jupiter and 13 m/s is the magnitude of the "wobble" of the Sun due to Jupiter's gravitational pull. Not all calculators will take the cube root of a number. Get help if yours does not. Put in your values for P and K and calculate the mass of this new planet in terms of the mass of Jupiter. That is, your calculations will give the mass of the planet as some factor times the mass of Jupiter (for example: Mplanet = 4 MJupiter). Show all work.