THE BEGINNINGS OF SCIENCE
IN EARLY GREECE

(c. 600 --- 400 BC)

"Atlas Brings Heracles the Apples of the Hesperides in the Presence of Athena,"
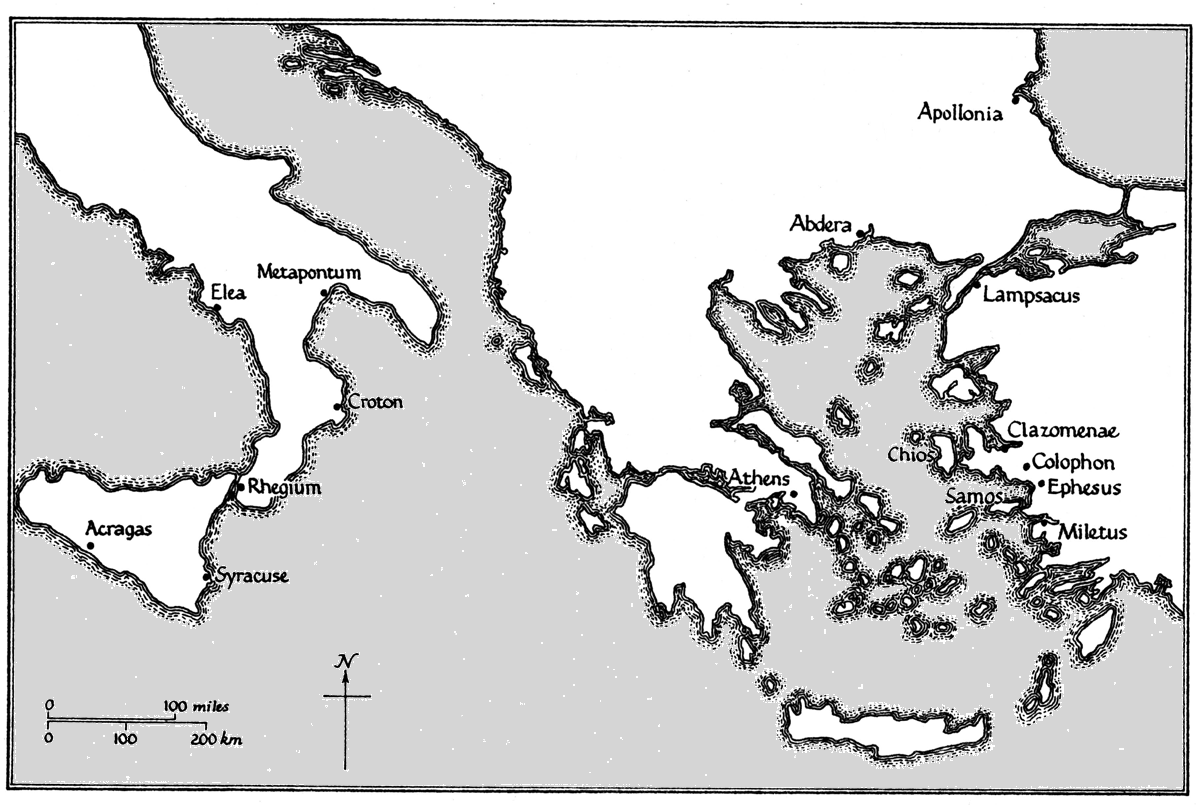
from the Temple of Zeus at Olympia,
c. 460 BC.

During this time, when gods embodied nature and interfered in human lives, the journey from mythos to logos began.

WHAT DO WE KNOW OF THE PRESOCRATIC PHILOSOPHERS?

• Not much ... not a single original work
  has survived intact for us to study!

• The only sources are

1. Fragments --- a few quotations from Presocratic works that have survived in works written later.

2. Testimonia --- comments in the writings of Plato and Aristotle on Presocratic ideas.

3. Doxography --- summaries and (summaries)² of Presocratic works.

adapted from http://www.forthnet.gr/presocratics/

EARLY GREEK MATHEMATICS

• arithmetic: the study of "multitude," or discrete quantity

started with the commerce and trade of Phoenician merchants

handicapped by the lack of efficient numeric and algebraic notation

• geometry: the study of "magnitude," or continuous quantity

geometry = "measurement of land,"

first arose in surveying practices among the ancient Egyptians

EARLY GREEK ARITHMETIC

The early Greeks proved a general rule for finding all sets of numbers

a, b, and c

such that

a² + b² = c²

(For example, 3² + 4² = 5²)

Recipe: take any two different whole numbers p and q, both even or both odd (say p = 3, and q = 1)

a = pq = 3(1) = 3

b = (p² - q²)/2 = (3² - 1²)/2 = 4

c = (p² + q²)/2 = (3² + 1²)/2 = 5

EARLY GREEK GEOMETRY

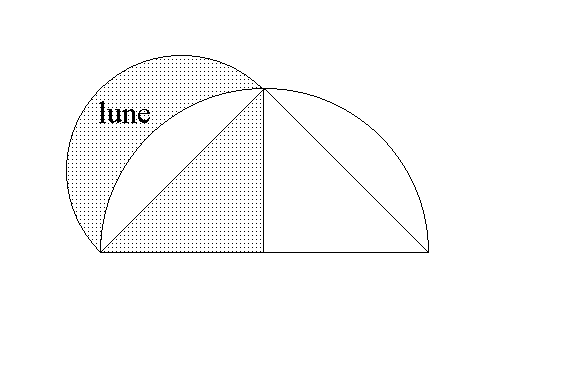
The "quadrature of the lune" was accomplished by Hippocrates of Chios (c. 440 B.C.)

Using only a compass (divider) and straightedge, Hippocrates determined how to construct a square whose area was equal to that of the lune

The early Greek philosophers sought natural, rather than supernatural, explanations for natural processes.

They believed the world is ordered and intelligible, rather than random and arbitrary. They asked the most fundamental questions:

What is the world made of?

Is the world changing or changeless and eternal?

Can something come from nothing?

How many things are there in the world?

For the concept of the universe, the whole of reality, the early Greek philosophers chose the word

"kosmos"

which derives from a word meaning

"to order"    "to arrange"    "to marshall"

But "kosmos" in everyday Greek also meant an adornment, as in our word "cosmetic."

The answers to their questions should not be merely ordered and logical, but beautiful and elegant as well.

Listen to Werner Heisenberg, a founder of quantum mechanics:

"If nature leads us to mathematical forms of great simplicity and beauty, ... to forms that no one has previously encountered, we cannot help thinking that they are 'true,' that they reveal a genuine feature of nature ... You must have felt this too: the almost frightening simplicity and wholeness of the relationships which nature suddenly spreads out before us and for which none of us was in the least prepared."

--- quoted in S. Chandrasekhar's Truth and Beauty

THALES OF MILETUS

624 --- 546 BC

• the first to ask, "What is the basic substance of the universe?"

• water is the source or material principle (arche) of everything

• earth is a flat disk floating on water

• said to have predicted a solar eclipse of 584 BC (probably myth)

• no difference between living and nonliving matter: "All things are full of gods." (~ life-germs?)
  

ANAXIMANDER OF MILETUS

610 --- 540 BC

• the first principle of all other things is the infinite "apeiron" (no single substance, indefinite)

• from this, the heavens and the worlds in them arise

• the earth is aloft, not supported by anything, because it is of equal distance from everything

• earth is cylindrical in shape
  

ANAXIMENES OF MILETUS

fl. c. 545 BC

• the infinite air is the source or material principle of everything

• air differs in its substantial properties by its rarity and density

when very attenuated, fire

when more condensed, wind and then cloud

and when still more condensed water and earth and stone

• the soul is like air in its nature
  

PYTHAGORAS OF SAMOS

570 --- 500 BC

• the Pythagoreans (~300) belonged to a semi-mystical scientific society (secret signs, ...)

• believed the brain is the location of the soul, and that the soul cyclically migrates among living forms

• forbade eating beans because they contain the souls of the dead

• "All is number" (from Pythagoras's observations in music, mathematics and astronomy)

• Each number has its own traits:

1: the number of reason

2: the first even or female number, the number of opinion

3: the first true male number, the number of harmony

4: the number of justice or retribution

5: marriage

6: creation

10: the perfect number, the number of the universe

• discovered that vibrating strings produce harmonious tones when the ratios of the lengths of the strings are whole numbers
  

HERACLITUS

fl. c. 500 BC (born in Ephesus)

• all things are an exchange of fire

• there are bowls in the heavens that catch fiery exhalations (stars)

• change is the most important principle of the universe

• "everything flows"

• change generated by opposites, stability achieved by balance

• universe eternal: no beginning, forever changing

• Heraclitus trusted his senses, observing the world in a state of never-ending flux.
  

Socrates comments on Heraclitus:

"They say that Euripedes gave [Socrates] a copy of Heraclitus' book and asked him what he thought of it. He replied: 'What I understand is splendid; and I think that what I don't understand is too --- but it would take a Delian diver to get to the bottom of it.'"

--- Diogenes Laertius, Lives of the Philosophers

The Milesian philosophers and Heraclitus believed in a basic substance at the source of all things.

But ... how can one substance change into something else?

How many things are there in the world?

Enter the Eleatics (~ 500 BC) from the Greek colony of Elea in southern Italy.

PARMENIDES OF ELEA

540 --- 480 BC

• nothing can come out of nothing

• everything in the world is eternal

• rejected the possibility of actual change

• our senses and observations of change are unreliable

• we follow the Way of Opinion (illusion), not the Way of Truth

• first to ask "Is it, or is it not?" of our perception of the world
  

ZENO OF ELEA

fl. c. 450 BC

• disciple of Parmenides (his "son")

• sought to disprove change

• believed that only one thing exists:

1. if any object is divisible into more than one thing, we can keep on dividing forever into an infinite number of smaller pieces

2. the sum of an infinite number of small (but not zero) pieces must be infinite in size --- an absurdity!

3. therefore nothing can be divisible; only one thing exists

 

F
I
N
I
S
H
                                                                                               Achilles and the Tortoise

• tortoise has a head start

• by the time A reaches where T is, T has moved on ...

• by the time A reaches where T is, T has moved on ...

• this happens again and again and ...

• so Achilles can never catch up to tortoise!

Let's assume that Achilles runs 1 m/s, and the tortoise runs 1/2 m/s.  If Achilles has to run 1 meter, and the tortoise has to run 1/2 meter, we expect them to reach the finish line at the same time.  Follow Zeno's argument.  I'll show Achilles as a blue vertical line that starts the race at 0, and the tortoise as a green vertical line that starts the race at 1/2 meter.

|      |     |     |      |     |     |      |     |      |     |     |      |     |     |      |     |
0                                            1/2 m                                           1 m
A starts at 0, T starts at 1/2 meter

|     |      |     |     |      |     |     |      |     |      |     |     |     |     |      |     |
0                                            1/2 m                                           1 m
A travels 1/2 meter, T is 1/4 meter ahead

|     |      |     |     |      |     |     |      |     |     |      |     |      |     |      |     |
0                                            1/2 m                                           1 m
A travels 1/4 meter, T is 1/8 meter ahead

|     |      |     |     |      |     |     |      |     |     |      |     |     |      |     |     |
0                                            1/2 m                                           1 m
A travels 1/8 meter, T is 1/16 meter ahead

Zeno's paradox says:

• subtract A - 1/2 A:

                                     A = 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + ...
                            - 1/2 A =           1/4 + 1/8 + 1/16 + 1/32 + ...

                              1/2 A = 1/2

• multiply each side by 2 to get A = 1

• thus Achilles has run A = 1 meter

• Achilles does not have to run an infinite distance to catch the tortoise, just 1 meter!

Oh, really? Suppose Achilles takes one step each time, and starts on his right foot:

R                                               L                      R          L    R..
|     |     |     |      |     |     |      |     |     |      |     |     |      |     |     |      |
0                                            1/2 m                                           1 m

Question: which foot is on the ground when Achilles has traveled one meter and caught the tortoise?

If you can't answer this question, then what does this say about the mathematical solution to Zeno's paradox?

• Are space and time infinitely divisible? Or is there a smallest non-zero unit of space? Of time?

• Mathematically, is there a smallest non-zero number (an infinitesimal)? Yes and no!)

In 1961 the logician Abraham Robinson (1918-74) showed that the notion of an infinitesimal was in fact logically consistent (but not required) and that, therefore, infinitesimals could be introduced as new kinds of numbers. This led to a novel way of presenting the calculus, called nonstandard analysis.

Back to our story ... Heraclitus says,

• "everything flows" (changes)

• our sensory perceptions are reliable

Parmenides says,

• nothing changes

• our sensory perceptions are unreliable

Empedocles realized that insisting on a single basic substance was the problem. No single basic substance could change into anything else and remain basic.

EMPEDOCLES

c. 492 --- 433 BC (born in Acragas)

• four primary and irreducible elements: earth, air, fire, and water

• physical world is made of these unchanging eternal elements in various changing combinations

• combinations of the four elements are determined by the interaction of Love (attraction) and Strife (repulsion) >>> chemistry!

• today we call them positive and negative electric charge (unlike charges attract, like charges repel)

ANAXAGORAS OF CLAZOMENAE

c. 500 --- 428 BC

• first philosopher of classical Athens

• the creative and driving force of the cosmos is Mind (nous)

• 

the first to realize the moon shines by reflected light from the "red-hot stone" (the sun)

• the first to explain correctly the reason for eclipses of the sun (the moon between Earth and sun) and eclipses of the moon (Earth's shadow hitting the moon)
  

DEMOCRITUS

c. 460 --- 370 BC (born in Abdera)

• believed that there must be indivisible bodies ("atoms")

• infinite divisibility could lead to a universe of objects of zero magnitude, a paradox since nothing can come from nothing

• an infinite variety of eternal atoms combines and dissolves according to their shape, order, and position (like Legos)

• the soul (not immortal) is made of round, smooth atoms

Galen (b. 129 AD) wrote, "... the primary element is qualityless, having no natural whiteness or blackness or any other color whatever, and no sweetness or bitterness or heat or cold or in general any other quality whatever. For, says Democritus,

'By convention color, by convention bitter, by convention sweet: in reality atoms and void.'

And he thinks that it is from the congregation of atoms that all the perceptive qualities came to be --- they are relative to us who perceive them, and in nature there is nothing white or black or yellow or red or bitter or sweet."

HOW NOW,
BROWN COW?

Is there a color "brown?"

In 1666 AD, Isaac Newton passed a ray of sunlight through a prism and split the white light into a rainbow spectrum of colors.

red, orange, yellow, green, blue, indigo, violet ...

All of these colors of light waves have their own unique wavelength.

• But there is no brown color in the spectrum! 

• no such thing as the wavelength of brown

• "brown" is our internal representation of the mixture of other colors

• the color brown is our invention, and begins and ends within our mind

• brown (and in fact all color) is the way our mind represents the physical property of the wavelength of a light wave

The limonene molecule (C₁₀H₁₆) exists in two forms that are mirror images of each other:

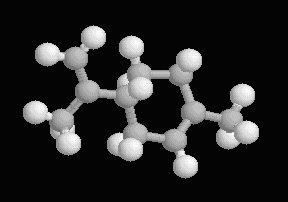l-limonene

---  smells piney, turpentine smell   

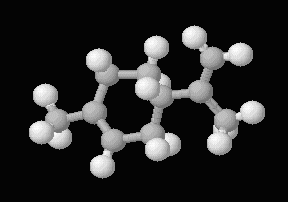d-limonene

--- pleasing orange scent                          

The scents are the mind's interpretation of molecules.

• Democritus believed everything we perceive is due to the movement of atoms through the void

• he understood that we have come to an accommodation with the exterior world of atoms

• all of our experience is with our internal interpretation of our sensory perceptions

• "In reality we know nothing --- the truth is in the depths."

• "The Truth is Out There" (Fox Mulder of The X-Files)

At the beginning of the 21^st century, can something come from nothing?

Is there such a thing as "nothing?"

The closest thing to "nothing" is the vacuum.

Today cosmologists are attempting to explain the creation of everything from nothing, from the vacuum.

The vacuum is not truly "nothing;" it is a state of minimum energy where quantum fluctuations, consistent with the Heisenberg's uncertainty principle, could have led to the formation of particles in the Big Bang that created both space and time.

"Creation" implies a time-ordering:

"first it is not, then it is"

Is it meaningful to say that time was created?

When was "is not?"

Is time t = 0 part of time or not?

As cosmologists push the frontiers of science, they ask Zeno questions.

At the beginning of the 21^st century, what is the fundamental component of the universe?

• atoms?

No, they were (and continue to be) manufactured by the nuclear reactions in the centers of stars.

• protons, neutrons, and electrons?

No, protons and neutrons are made of quarks and held together by other particles. All in all, there are far too many particles for any of them to be fundamental.

Best Guess: Strings!

• instead of many types of point-like elementary particles, some physicists postulate that in nature there is a single variety of string-like object

• the string is not made up of anything; rather, it is basic and other things are made up of it

• as with musical strings, this basic string can vibrate, and each vibrational mode can be viewed as a point-like elementary particle, just as the harmonics of a musical string are perceived as distinct notes!

Pythagoras would have been pleased

Some references for this presentation:

• Atchity, Kenneth J., The Classical Greek Reader, Oxford University Press, 1996

• Barnes, Jonathan, Early Greek Philosophy, Penguin Classics, 1987

• Chandrasekhar, S., Truth and Beauty : Aesthetics and Motivations in Science, U. Chicago Press, 1991

• Dunham, William, Journey Through Genius : The Great Theorems of Mathematics, Penguin, 1991

• Gaarder, Jostein, Sophie's World, Berkley Books, 1996

• Hertherington, Morriss S.,  Cosmology, Garland Publishing, 1993

• Lindberg, David C., The Beginnings of Western Science, U. Chicago Press, 1992

• Sacks, Oliver, The Man Who Mistook His Wife for a Hat, Harper and Row, 1987

• Sainsbury, R. M., Paradoxes, Cambridge U. Press, 1995

Return to Greek Home page

Return to Brad Carroll's Home page

Go to the Physics Department Home page

Go to the WSU Home page

e-mail comments to:  bcarroll@weber.edu